Question

giúp em mấy câu này nữa được không ạ?

c1 : |x-4|(x-2)=m có 3 no pb?

c2:biết pt: x²-xcos(a)+sin(a)-1=0 luôn có no p và q với mọi a.tìm hệ thức liên hệ giữa p và q độc lập với a?     

 A.6(pq)²-3(4p+2q-1)²=1   B.p+q=1   C.p-q=pq   D.p=q

 

c3:tìm đk của m để pt sau có no: $\sqrt{5x^2-5x-m+3}$=2x-3 ?

c4:tìm để pt: x²-4x+4-m=0 có nghiệm >5.

c5: hàm số y= x²-(m+5)x+10 luôn cắt y=5 tại điểm của hoàng độ bằng?

c6: cho x²-2mx -2=0, tìm m để S=(x₁²+9)(x₂²+1) có gt nhỏ nhất?

Answer 1

Câu 1:

Dựa vào đồ thị để phương trình có 3 nghiệm phân biệt khi 0< m < 1

  

Answer 2

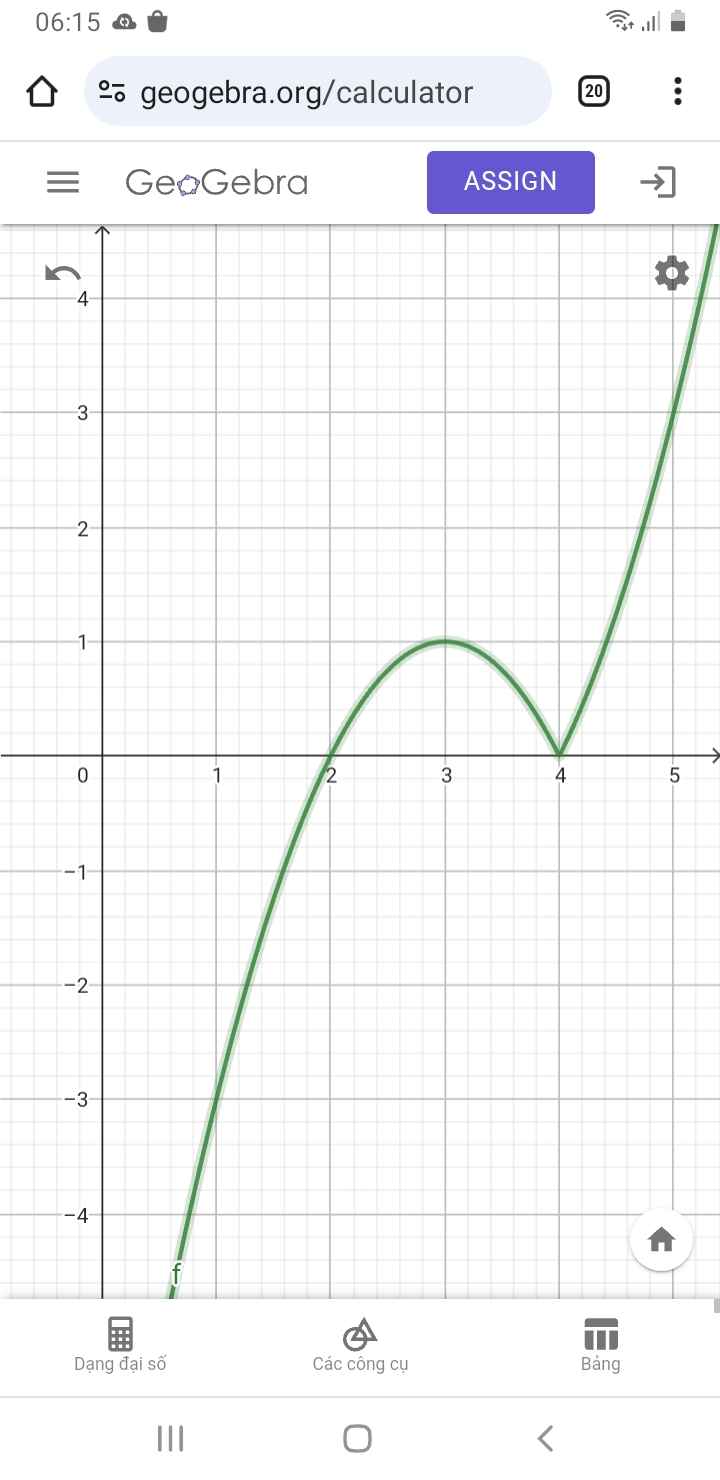
2.

Theo hệ thức Viet: \(\left\{{}\begin{matrix}p+q=cosa\\p.q=sina-1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}p+q=cosa\\pq+1=sina\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(p+q\right)^2=cos^2a\\\left(pq+1\right)^2=sin^2a\end{matrix}\right.\)

Cộng vế:

\(\left(p+q\right)^2+\left(pq+1\right)^2=cos^2a+sin^2a\)

\(\Leftrightarrow\left(p+q\right)^2+\left(pq+1\right)^2=1\)

Ko có hệ thức nào đúng cả

Answer 3

3.

\(\sqrt{5x^2-5x-m+3}=2x-3\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3\ge0\\5x^2-5x-m+3=\left(2x-3\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x^2+7x-6=m\end{matrix}\right.\)

\(\Leftrightarrow x^2+7x-6=m\) có nghiệm \(x\ge\dfrac{3}{2}\)

Ta có đồ thị hàm \(y=x^2+7x-6\) có dạng:

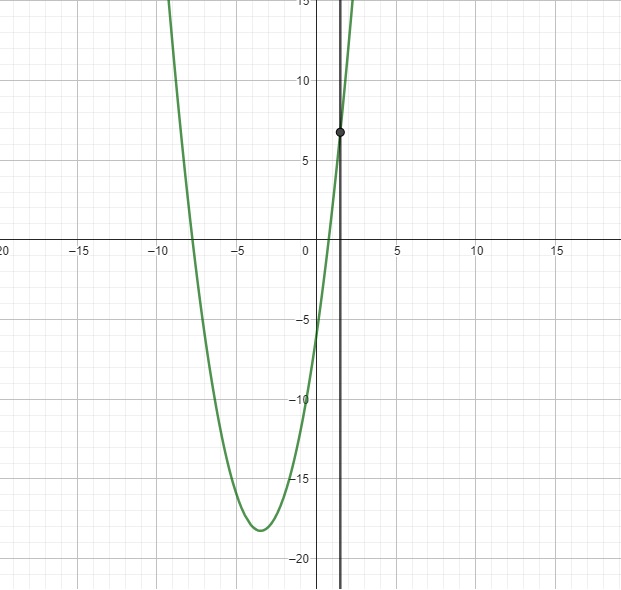
Tại \(x=\dfrac{3}{2}\Rightarrow y=\left(\dfrac{3}{2}\right)^2+7.\dfrac{3}{2}-6=\dfrac{27}{4}\)

\(\Rightarrow y=m\) cắt \(y=x^2+7x-6\) tại ít nhất 1 điểm thỏa mãn \(x\ge\dfrac{3}{2}\)

\(\Rightarrow m\ge\dfrac{27}{4}\)

Vậy với \(m\ge\dfrac{27}{4}\) thì pt có nghiệm

Answer 4

4.

\(x^2-4x+4-m=0\) có nghiệm \(x>5\)

\(\Leftrightarrow x^2-4x+4=m\) có nghiệm \(x>5\)

Hàm \(y=x^2-4x+4\) đồng biến khi \(x>2\) và \(y\left(5\right)=9\)

\(\Rightarrow x^2-4x+4=m\) có nghiệm \(x>5\) khi \(m>9\)

Em có thể vẽ đồ thị để giải nhưng ko cần thiết lắm

Answer 5

6.

\(x^2-2mx-2=0\)

\(ac=-2< 0\) nên pt luôn có 2 nghiệm pb trái dấu

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-2\end{matrix}\right.\)

Do \(x_1x_2=-2\Rightarrow x_2=-\dfrac{2}{x_1}\)

\(\Rightarrow S=\left(x_1^2+9\right)\left(\dfrac{4}{x_1^2}+1\right)=13+x_1^2+\dfrac{36}{x_1^2}\ge13+2\sqrt{x_1^2.\dfrac{36}{x_1^2}}=25\)

Dấu "=" xảy ra khi:

\(x_1^2=\dfrac{36}{x_1^2}\Rightarrow x_1^2=6\)

\(\Rightarrow\left[{}\begin{matrix}x_1=\sqrt{6}\Rightarrow x_2=-\dfrac{2}{\sqrt{6}}=-\dfrac{\sqrt{6}}{3}\\x_1=-\sqrt{6}\Rightarrow x_2=-\dfrac{2}{-\sqrt{6}}=\dfrac{\sqrt{6}}{3}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{x_1+x_2}{2}=\dfrac{\sqrt{6}}{3}\\m=\dfrac{x_1+x_2}{2}=-\dfrac{\sqrt{6}}{3}\end{matrix}\right.\)