Question

giúp em câu c với ạ!

Answer 1

Answer 2

c.

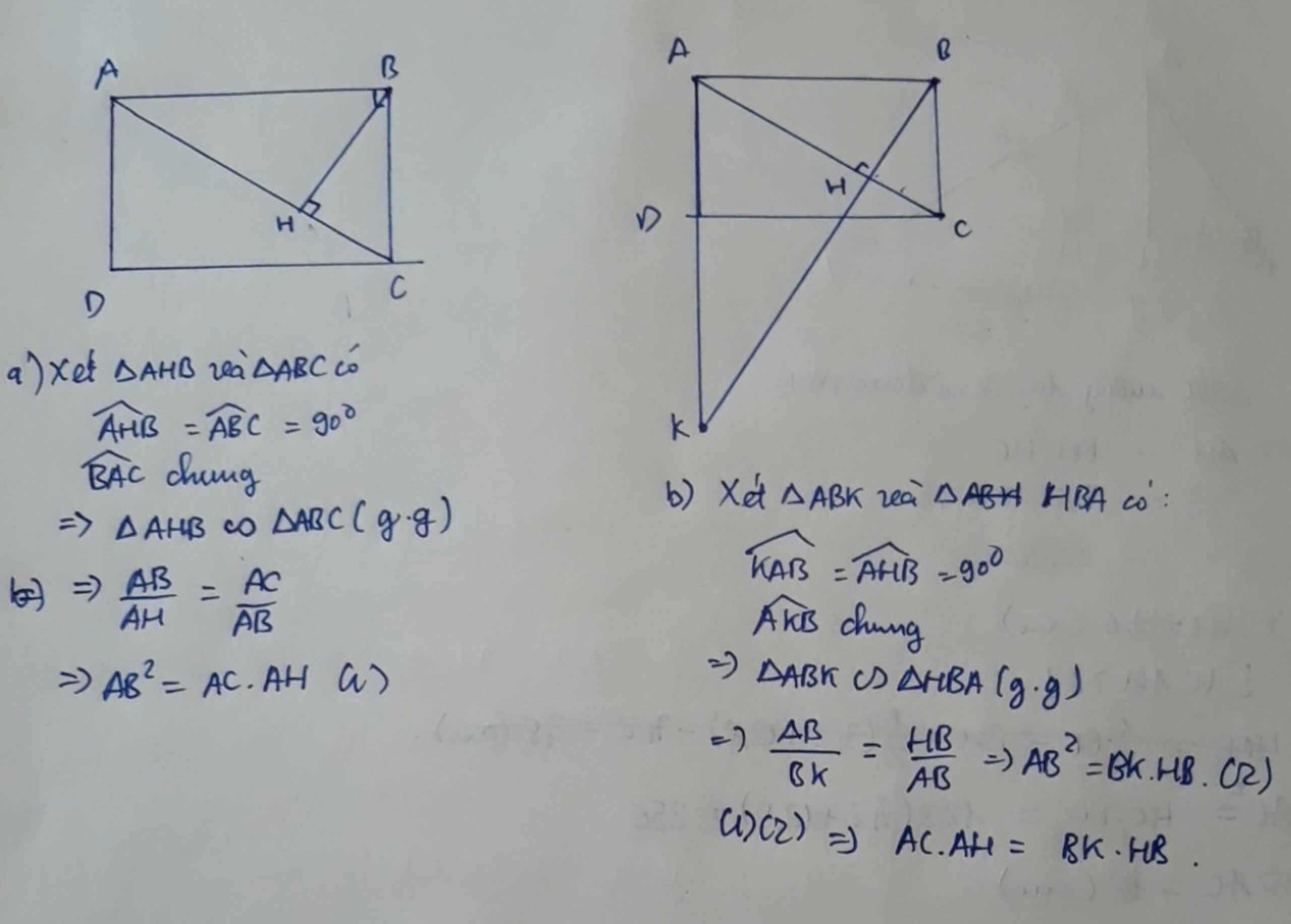
Xét hai tam giác ADC và AHK có:

\(\left\{{}\begin{matrix}\widehat{ADC}=\widehat{AHK}=90^0\\\widehat{DAC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow\Delta ADC\sim\Delta AHK\left(g.g\right)\)

\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AC}{AK}\Rightarrow AD.AK=AH.AC\)

Kết hợp câu a \(\Rightarrow AD.AK=AB^2=DC^2\)

\(\Rightarrow\dfrac{AK}{AD}=\dfrac{DC^2}{AD^2}=\left(\dfrac{DC}{AD}\right)^2\) (1)

Mà tam giác ADC vuông tại D \(\Rightarrow tan\widehat{DAC}=\dfrac{DC}{AD}\) (2)

(1);(2) \(\Rightarrow\dfrac{AK}{AD}=tan^2\widehat{DAC}\)