`1)P:(4x^2-16)/(2x+1)=(4x^2+4x+1)/(x-2)`
`=>P=(4x^2+4x+1)/(x-2)*(4x^2-16)/(2x+1)`
`=>P=(2x+1)^2/(x-2)*(4(x^2-4))/(2x+1)`
`=>P=(2x+1)^2/(x-2)*(4(x-2)(x+2))/(2x+1)`
`=>P=(2x+1)*4(x+2)`
`=>P=4(2x^2+5x+2)`
`=>P=8x^2+20x+8`
`2)(2x^2+4x+8)/(x^3-3x^2-x+3):P=(x^3-8)/((x+1)(x-3))`
`=>P=(2x^2+4x+8)/(x^3-3x^2-x+3):(x^3-8)/((x+1)(x-3))`
`=>P=(2(x^2+2x+4))/((x^2-1)(x-3))*((x+1)(x-3))/((x-2)(x^2+2x+4))`
`=>P=(2(x^2+2x+4))/((x-1)(x+1)(x-3))*((x+1)(x-3))/((x-2)(x^2+2x+4))`
`=>P=2/((x-1)(x-2))`
`=>P=2/(x^2-3x+2)`
1: \(P:\dfrac{4x^2-16}{2x+1}=\dfrac{4x^2+4x+1}{x-2}\)
=>\(P:\dfrac{4\left(x-2\right)\left(x+2\right)}{2x+1}=\dfrac{\left(2x+1\right)^2}{x-2}\)
=>\(P=\dfrac{\left(2x+1\right)^2}{x-2}\cdot\dfrac{4\left(x-2\right)\left(x+2\right)}{2x+1}=\dfrac{4\left(x+2\right)\left(2x+1\right)}{1}\)
=>\(P=4\left(2x^2+5x+2\right)=8x^2+20x+8\)
2: \(\dfrac{2x^2+4x+8}{x^3-3x^2-x+3}\cdot P=\dfrac{x^3-8}{\left(x+1\right)\left(x-3\right)}\)
=>\(\dfrac{2\left(x^2+2x+4\right)}{x^2\left(x-3\right)-\left(x-3\right)}\cdot P=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x+1\right)\left(x-3\right)}\)
=>\(P=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x+1\right)\left(x-3\right)}:\dfrac{2\left(x^2+2x+4\right)}{\left(x-3\right)\left(x-1\right)\left(x+1\right)}\)
=>\(P=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x+1\right)\left(x-3\right)}\cdot\dfrac{\left(x-3\right)\left(x-1\right)\left(x+1\right)}{2\left(x^2+2x+4\right)}\)
=>\(P=\dfrac{\left(x-2\right)\left(x-1\right)}{2}\)
3: \(\dfrac{x-y}{x^3+y^3}\cdot Q=\dfrac{x^2-2xy+y^2}{x^2-xy+y^2}\)
=>\(Q\cdot\dfrac{x-y}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{\left(x-y\right)^2}{x^2-xy+y^2}\)
=>\(Q\cdot\dfrac{1}{x+y}=x-y\)
=>\(Q=\left(x-y\right)\left(x+y\right)=x^2-y^2\)
4: \(\dfrac{x+y}{x^3-y^3}\cdot Q=\dfrac{3x^2+3xy}{x^2+xy+y^2}\)
=>\(Q\cdot\dfrac{x+y}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{3x\left(x+y\right)}{x^2+xy+y^2}\)
=>\(Q\cdot\dfrac{1}{x-y}=3x\)
=>\(Q=3x:\dfrac{1}{x-y}=3x\left(x-y\right)\)







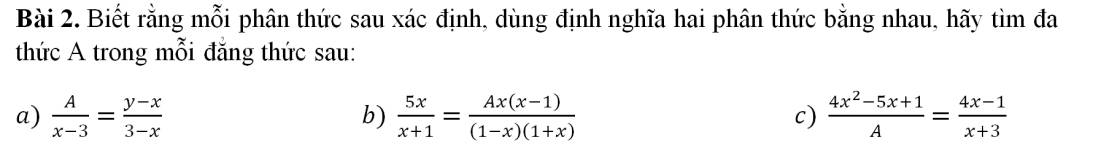 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 


 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ



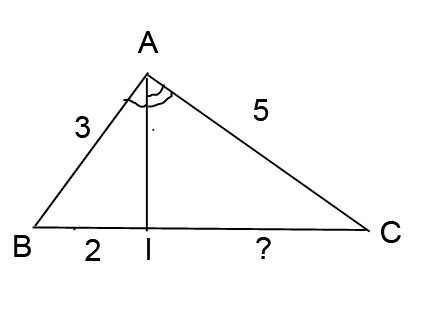 giúp em bài này với ạ
giúp em bài này với ạ





