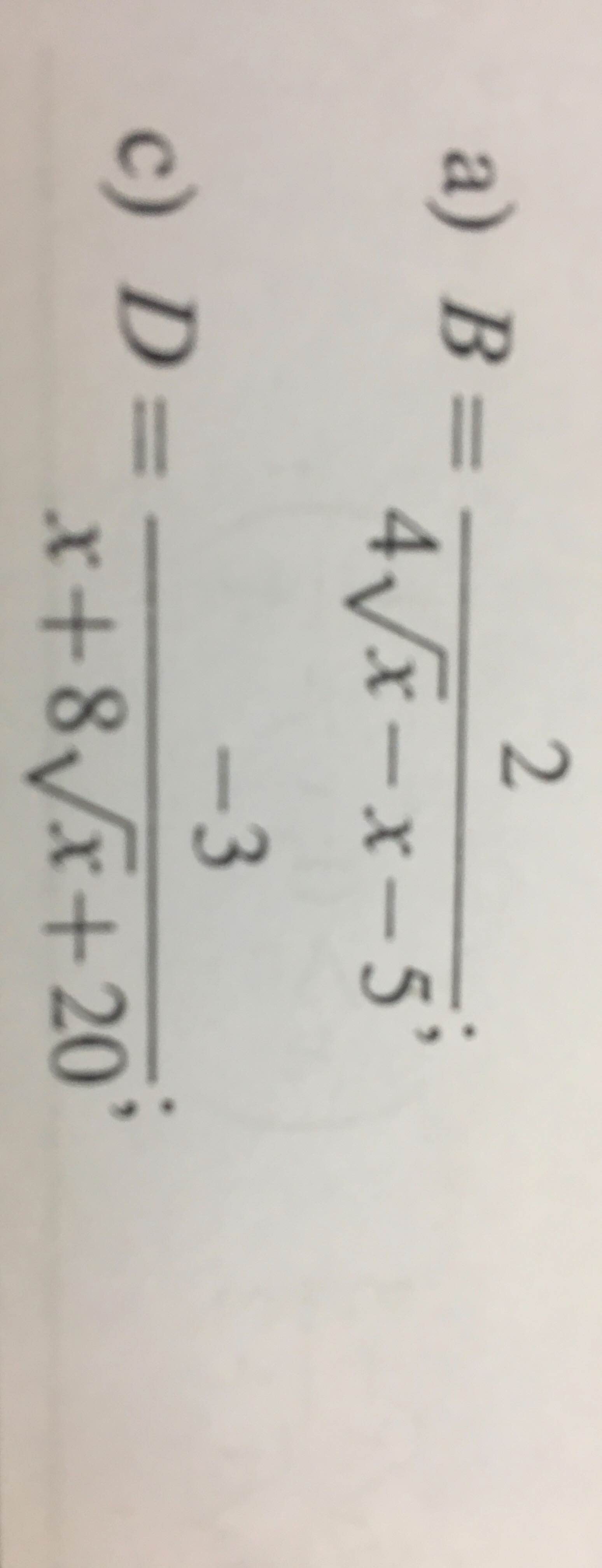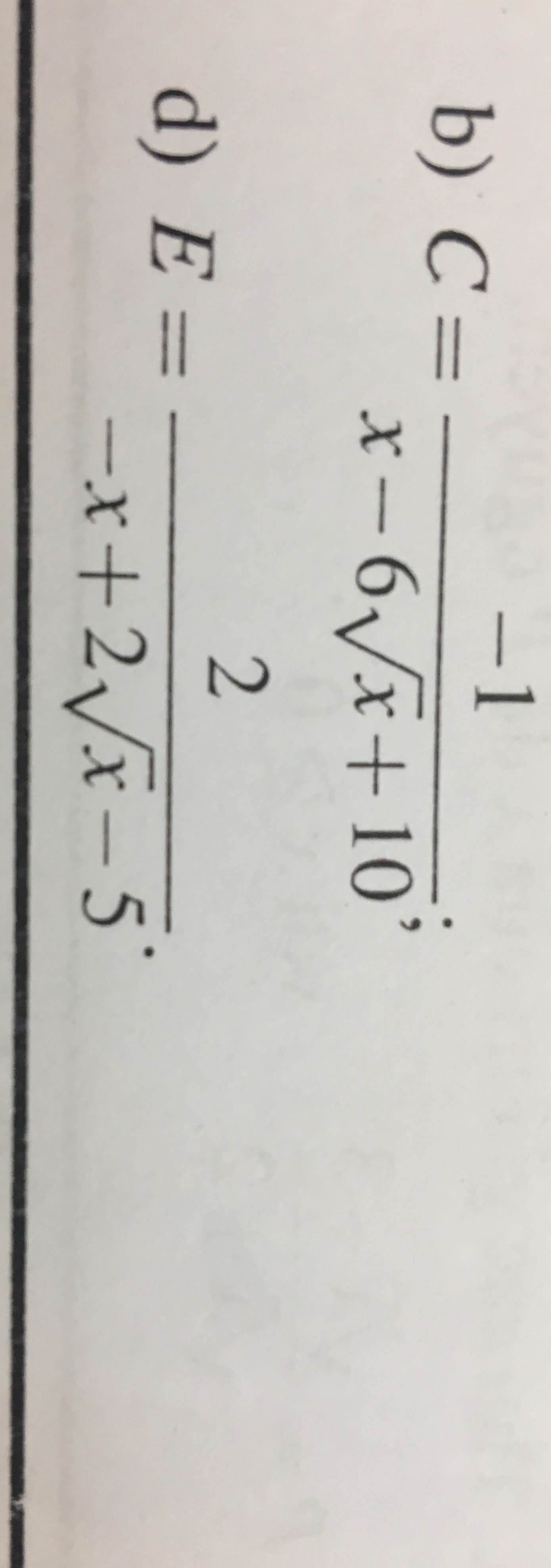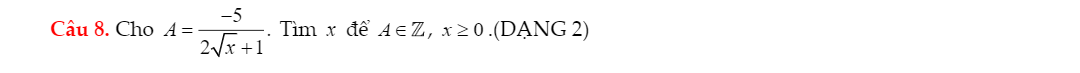\(B=\dfrac{2}{-1-\left(x-4\sqrt{x}+4\right)}=\dfrac{2}{-1-\left(\sqrt{x}-2\right)^2}\ge\dfrac{2}{-1}=-2\)
\(B_{min}=-2\) khi \(x=4\)
\(D=\dfrac{-3}{x+8\sqrt{x}+20}\ge-\dfrac{3}{20}\)
\(D_{min}=-\dfrac{3}{20}\) khi \(x=0\)
\(A=\dfrac{2}{4\sqrt{x}-x-5}=\dfrac{2}{-\left(x-4\sqrt{x}+4+1\right)}=\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\)
\(-\left(\sqrt{x}-2\right)^2-1\le-1\\ \Leftrightarrow\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\ge-2\)
Dấu \("="\Leftrightarrow x=4\)
\(B=\dfrac{-3}{x+8\sqrt{x}+20}=\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\)
\(\left(\sqrt{x}+4\right)^2+4\ge4\\ \Leftrightarrow\dfrac{3}{\left(\sqrt{x}+4\right)^2+4}\le\dfrac{3}{4}\\ \Leftrightarrow\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\ge-\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\sqrt{x}+4=0\Leftrightarrow x\in\varnothing\)
Vậy dấu \("="\) không xảy ra