Bài 6:
\(\dfrac{x-1}{2013}+\dfrac{x-2}{2012}+\dfrac{x-3}{2011}=\dfrac{x-4}{2010}+\dfrac{x-5}{2009}+\dfrac{x-6}{2008}\)
⇔\(\dfrac{x-1}{2013}-1+\dfrac{x-2}{2012}-1+\dfrac{x-3}{2011}-1=\dfrac{x-4}{2010}-1+\dfrac{x-5}{2009}-1+\dfrac{x-6}{2008}-1\)⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}=\dfrac{x-2014}{2010}+\dfrac{x-2014}{2009}+\dfrac{x-2014}{2008}\)
⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}-\dfrac{x-2014}{2010}-\dfrac{x-2014}{2009}-\dfrac{x-2014}{2008}=0\)
⇔\(\left(x-2014\right)\left(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
Vì \(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\ne0\)
\(\Rightarrow x-2014=0\)
⇔\(x=2014\).
-Vậy \(S=\left\{2014\right\}\).
Bài 7:
\(x^2-4x+y^2-6y+15=2\)
⇔\(x^2-4x+y^2-6y+15-2=0\)
⇔\(x^2-4x+y^2-6y+13=0\)
⇔\(\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
⇔\(\left(x-2\right)^2+\left(y-3\right)^2=0\)
Vì \(\left(x-2\right)^2\ge0,\left(y-3\right)^2\ge0\).
\(\Rightarrow\)\(\left(x-2\right)^2=0\) và \(\left(y-3\right)^2=0\)
⇔\(x=2\) và \(y=3\).
Bài 8:
\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)
⇔\(\left(x^2+1\right)^2+2x\left(x^2+1\right)+x^2+x\left(x^2+1\right)+x^2=0\)
⇔\(\left(x^2+1+x\right)^2+x\left(x^2+1+x\right)=0\)
⇔\(\left(x^2+1+x\right)\left(x^2+1+x+x\right)=0\)
⇔\(x^2+x+1=0\) (vô nghiệm, bạn tự c/m) hay \(x^2+2x+1=0\)
⇔\(x^2+2x+1=0\)
⇔\(\left(x+1\right)^2=0\)
⇔\(x=-1\).
-Vậy \(S=\left\{-1\right\}\)






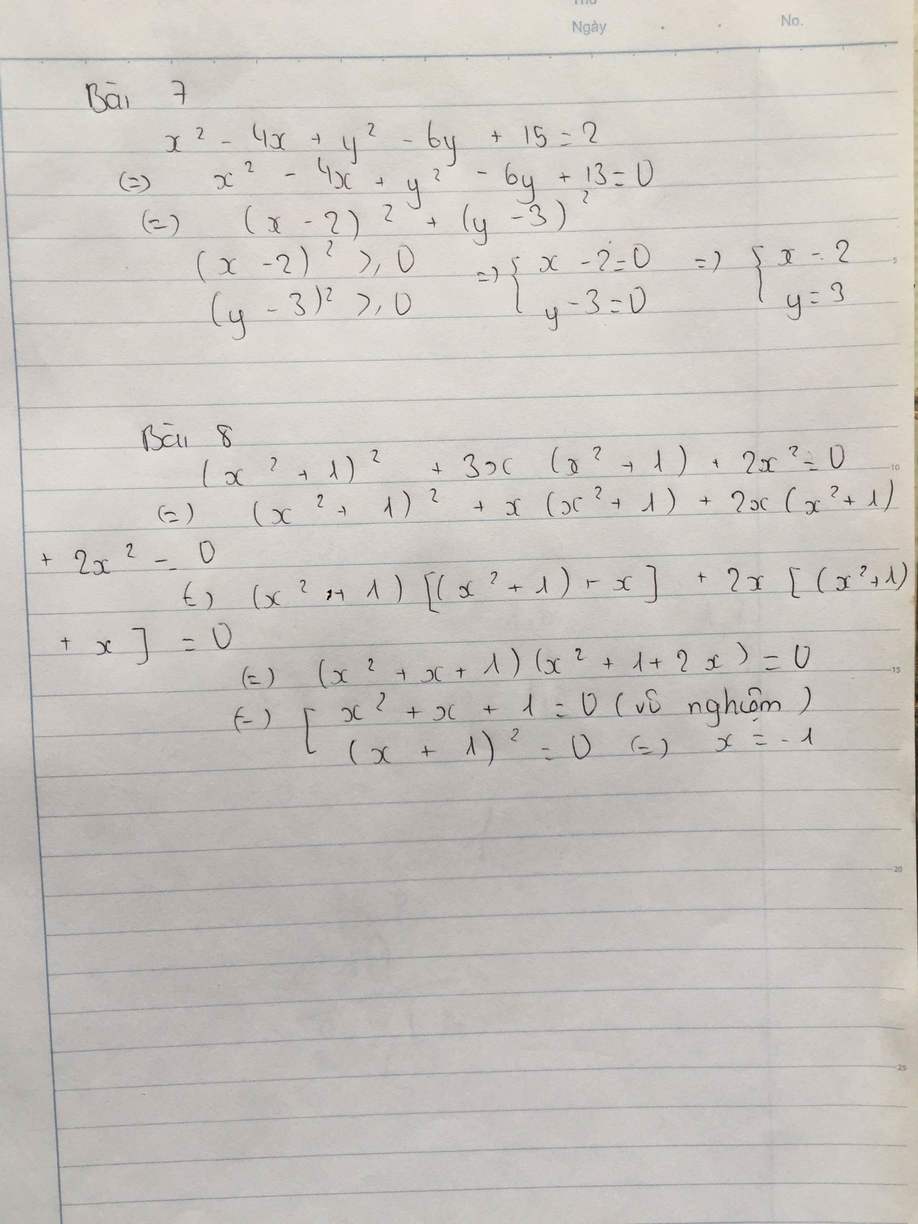



 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp

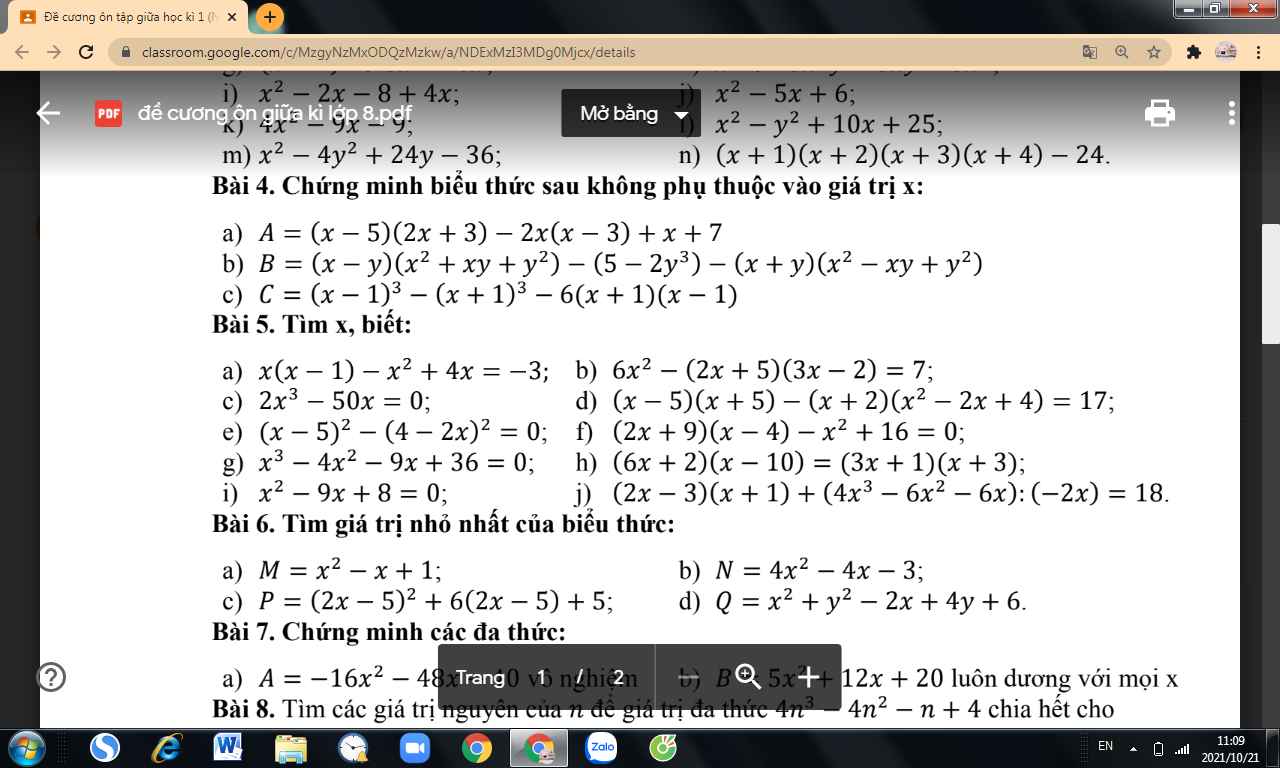
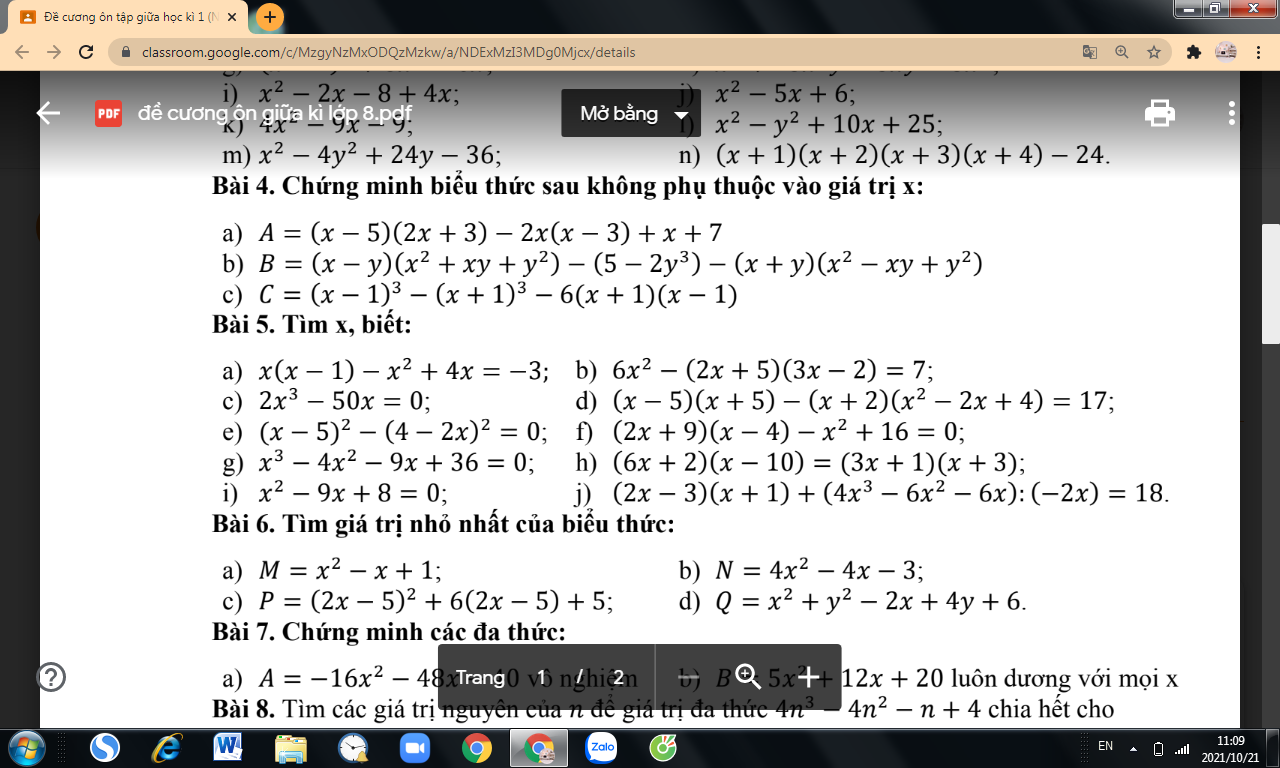


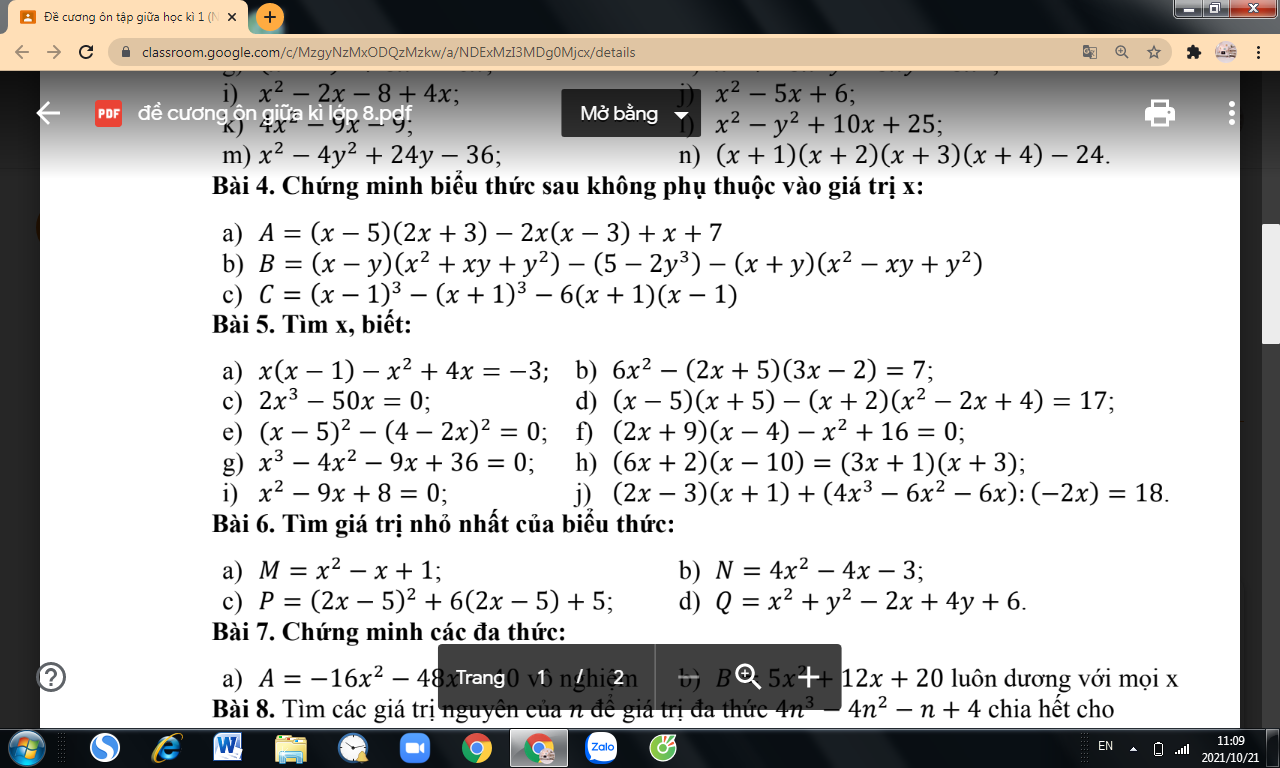

 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ


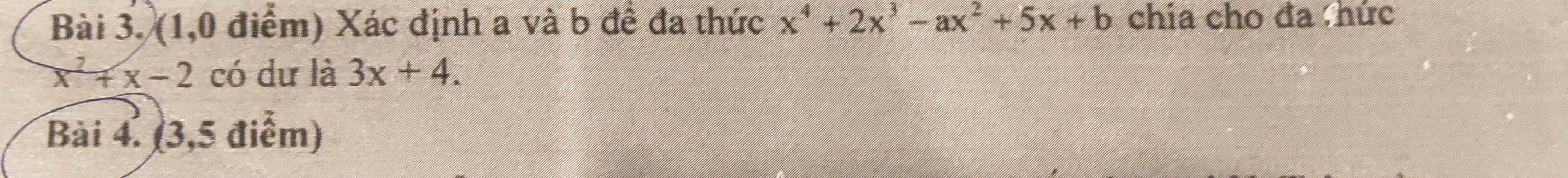 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp.