\(a,P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\\ =\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}\\ =\dfrac{x-1}{\sqrt{x}}\)
__
\(\dfrac{x-1}{\sqrt{x}}< 2\\ \Leftrightarrow\dfrac{x-1}{\sqrt{x}}< \dfrac{2\sqrt{x}}{\sqrt{x}}\\ \Leftrightarrow x-1< 2\sqrt{x}\\ \Leftrightarrow x-2\sqrt{x}-1< 0\\ \Leftrightarrow x-2\sqrt{x}+1-2< 0\\ \Leftrightarrow\left(\sqrt{x}-1\right)^2< 2\\ \Leftrightarrow\left|\sqrt{x}-1\right|< \sqrt{2}\\ \Leftrightarrow-2< \sqrt{x}-1< \sqrt{2}\\ \Leftrightarrow0< \sqrt{x}< \sqrt{2}+1\\ \Leftrightarrow0< x< \left(\sqrt{2}+1\right)^2\left(x\ge0;x\ne1\right)\)

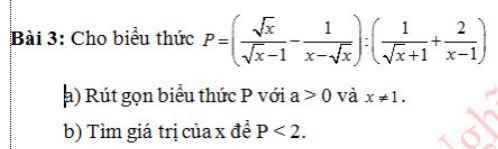



















 giúp e vs ạ :<
giúp e vs ạ :<