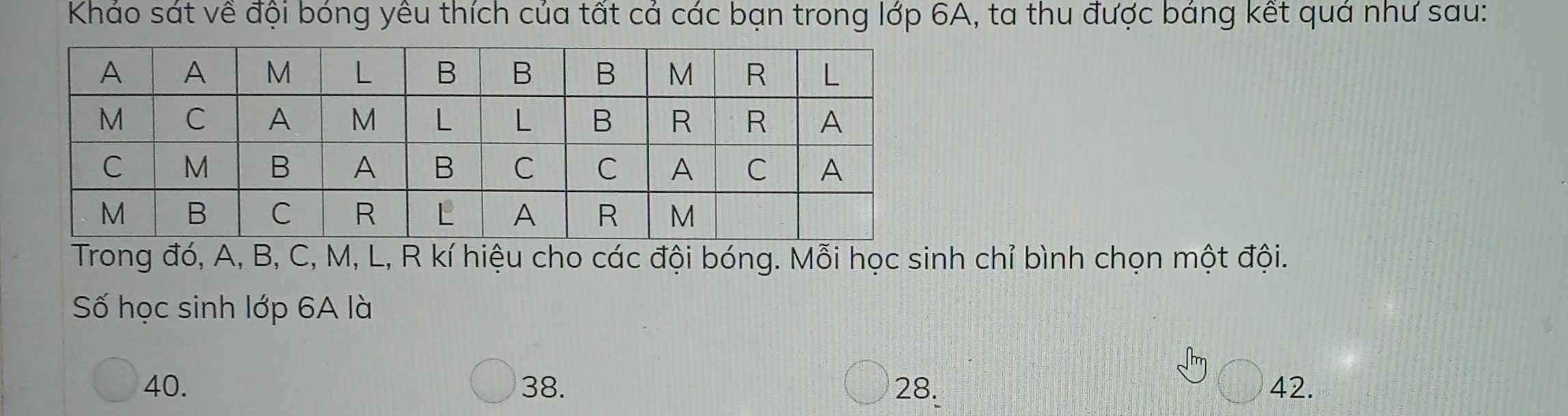
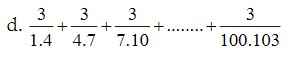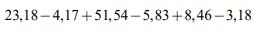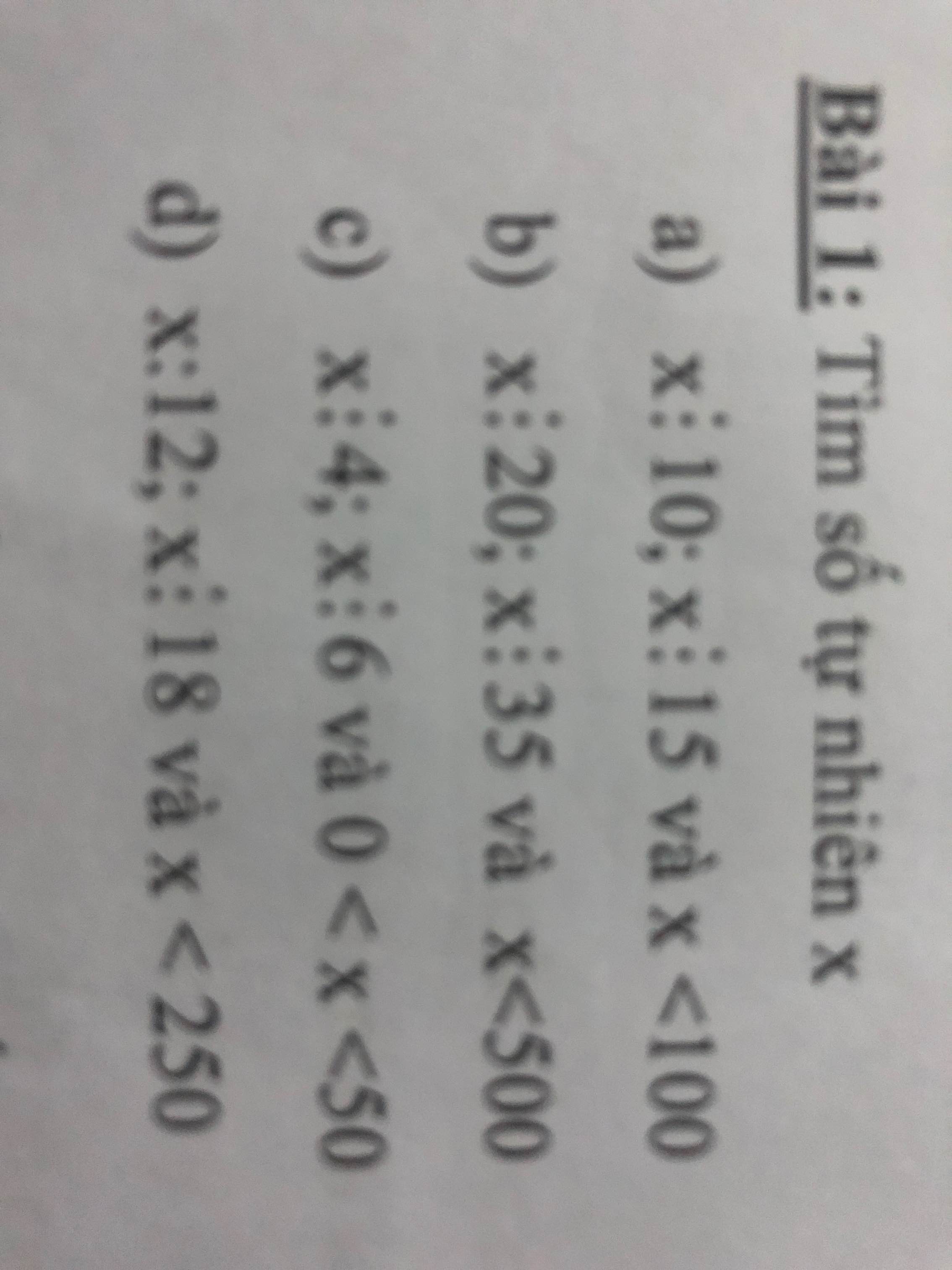\(\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{97}+\dfrac{1}{99}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{96}+\dfrac{1}{98}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{98}+\dfrac{1}{99}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{98}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{98}+\dfrac{1}{99}-1-\dfrac{1}{2}-...-\dfrac{1}{49}\)
\(=\dfrac{1}{50}+\dfrac{1}{51}+...+\dfrac{1}{99}\)
Đúng 0
Bình luận (0)
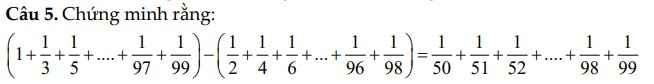
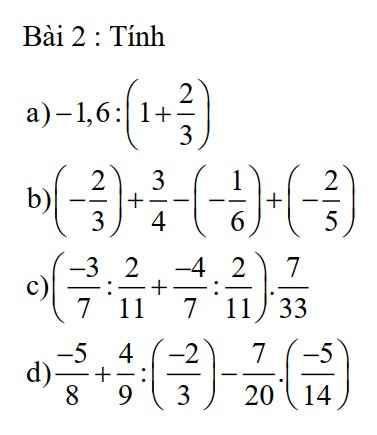giúp với giúp với giúp e với ạ. e cảm ơn
