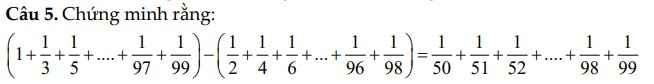\(a,A=2^0+2^1+2^2+...+2^{2006}\\ \Rightarrow2A=2^1+2^2+...+2^{2007}\\ \Rightarrow2A-A=2^1+2^2+...+2^{2007}-2^0-2^1-...-2^{2006}\\ \Rightarrow A=2^{2007}-1\)
\(b,B=1+3+3^2+...+3^{100}\\ \Rightarrow3B=3+3^2+...+3^{101}\\ \Rightarrow3B-B=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\\ \Rightarrow2B=3^{101}-1\\ \Rightarrow B=\dfrac{3^{101}-1}{2}\)
Đúng 6
Bình luận (0)
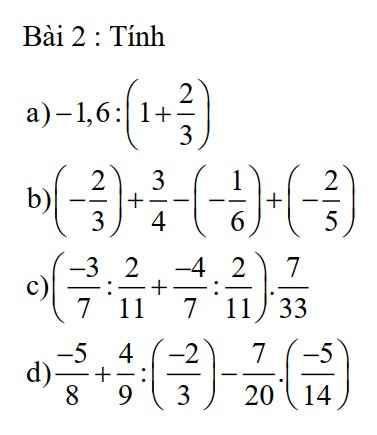giúp với giúp với giúp e với ạ. e cảm ơn
