a: ĐKXĐ: \(x\notin\left\{-1;-2;-3;-4\right\}\)
\(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}=\dfrac{1}{6}\)
=>\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
=>\(\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\)
=>\(\left(x+4\right)\left(x+1\right)=18\)
=>\(x^2+5x-14=0\)
=>(x+7)(x-2)=0
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
b: ĐKXĐ: x<>0
\(\dfrac{x+1}{x^2+x+1}-\dfrac{x-1}{x^2-x+1}-\dfrac{4}{x^5+x^3+x}=0\)
=>\(\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}-\dfrac{4}{x\left(x^4+x^2+1\right)}=0\)
=>\(\dfrac{x^3+1-x^3+1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{4}{x\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
=>\(\dfrac{2}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{4}{x\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
=>2x=4
=>x=2(nhận)
c:
ĐKXĐ: \(x\notin\left\{-9;-10\right\}\)
\(\dfrac{x+9}{10}+\dfrac{x+10}{9}=\dfrac{9}{x+10}+\dfrac{10}{x+9}\)
=>\(\left(\dfrac{x+9}{10}+1\right)+\left(\dfrac{x+10}{9}+1\right)=\left(\dfrac{9}{x+10}+1\right)+\left(\dfrac{10}{x+9}+1\right)\)
=>\(\dfrac{x+19}{10}+\dfrac{x+19}{9}-\dfrac{x+19}{x+10}-\dfrac{x+19}{x+9}=0\)
=>\(\left(x+19\right)\left(\dfrac{1}{10}+\dfrac{1}{9}-\dfrac{1}{x+10}-\dfrac{1}{x+9}\right)=0\)
=>\(\left(x+19\right)\left(\dfrac{x+10-10}{10\left(x+10\right)}+\dfrac{x+9-9}{9\left(x+9\right)}\right)=0\)
=>\(x\left(x+19\right)\left(\dfrac{1}{10\left(x+10\right)}+\dfrac{1}{9\left(x+9\right)}\right)=0\)
=>x(x+19)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-19\left(nhận\right)\end{matrix}\right.\)
a)
\(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}=\dfrac{1}{6}\left(x\ne-1;-2;-3;-4\right)\\ \Leftrightarrow\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}\\ \Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\\ \Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\\ \Leftrightarrow\left(x+1\right)\left(x+4\right)=18\\ \Leftrightarrow x^2+5x+4-18=0\\ \Leftrightarrow x^2+5x-14=0\\ \Leftrightarrow\left(x-2\right)\left(x+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-7\end{matrix}\right.\left(tm\right)\)
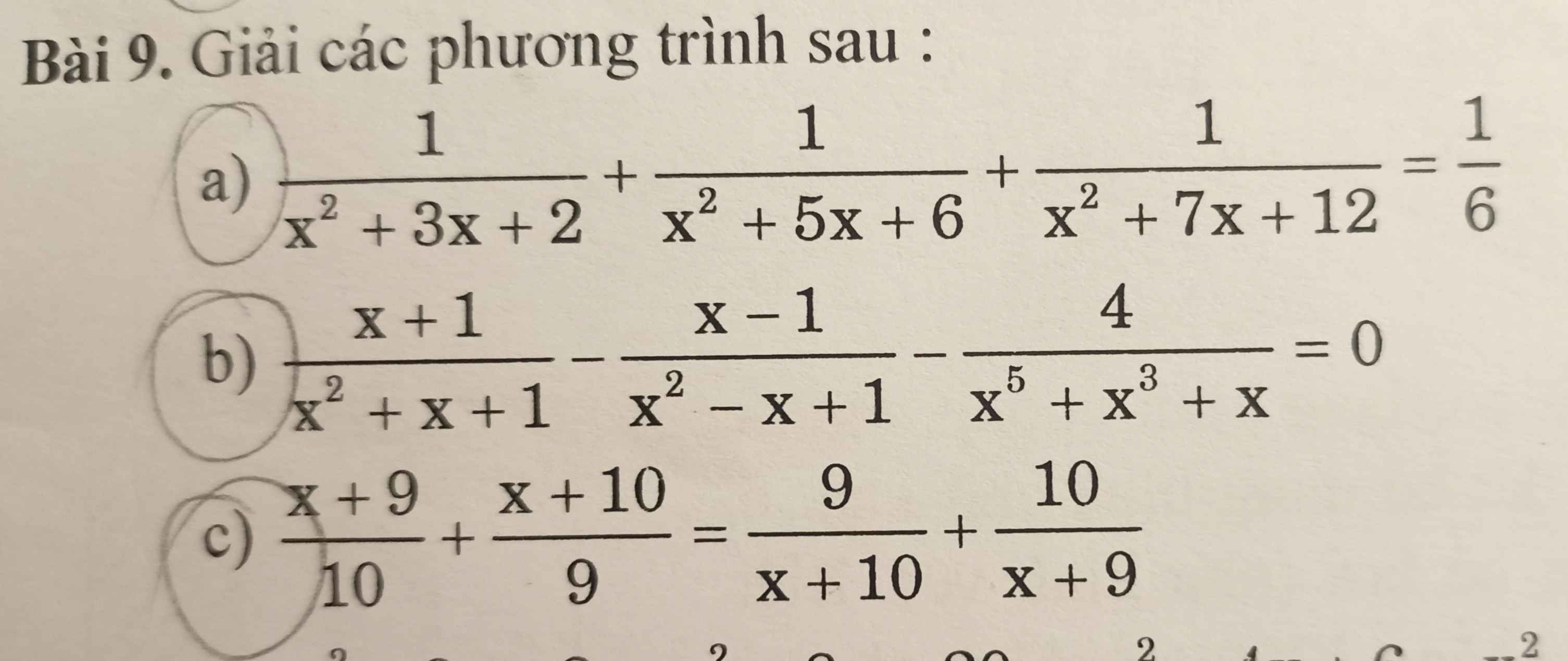
Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai