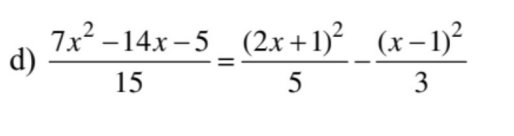\(\dfrac{7x^2-14x-5}{15}=\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}\)
=>\(\dfrac{7x^2-14x-5}{15}=\dfrac{3\left(2x+1\right)^2-5\left(x-1\right)^2}{15}\)
=>\(\dfrac{7x^2-14x-5}{15}=\dfrac{3\left(4x^2+4x+1\right)-5\left(x^2-2x+1\right)}{15}\)
=>\(7x^2-14x-5=12x^2+12x+3-5x^2+10x-5\)
=>\(7x^2-14x-5=7x^2+22x-2\)
=>22x-2=-14x-5
=>36x=-3
=>\(x=-\dfrac{3}{36}=-\dfrac{1}{12}\)
\(\dfrac{4x^2+4x+1}{5} - \dfrac{x^2 - 2x + 1}{3}\)
\(15. \dfrac{7x^2 - 14x - 5}{15} = 15 . ( \dfrac{4x^2 + 4x + 1}{5} - \dfrac{x^2 - 2x + 1}{3})\)
` 7x^2 - 14x -5 = 3(4x^2 + 4x + 1) - 5(x^2 - 2x + 1) `
` 7x^2 - 14x - 5 = 12x^2 + 12x + 3 - 5x^2 + 10x - 5 `
` 7x^2 -14x -5 = ( 12x^2 -5x^2) + (12x + 10x) + ( 3-5) `
` 7x^2 - 14x - 5 = 7x^2 + 22x - 2 `
` 7x^2 - 7x^2 - 14x - 22x = -2 + 5 `
` -36x = 3 `
` => x = -1/12 `
\(d,\dfrac{7x^2-14x-5}{15}=\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}\\ \dfrac{7x^2-14x-5}{15}=\dfrac{3\left(4x^2+4x+1\right)}{15}-\dfrac{5\left(x^2-2x+1\right)}{15}\\ \dfrac{7x^2-14x-5}{15}=\dfrac{12x^2+12x+3-5x^2+10x-5}{15}\\ 7x^2-14x-5=7x^2+22x-2\\ -14x-22x=-2+5\\ -36x=3\\ x=-\dfrac{1}{12}\)