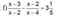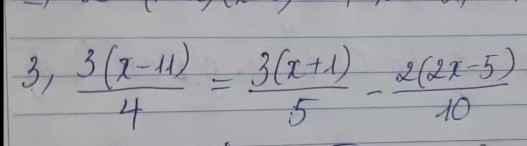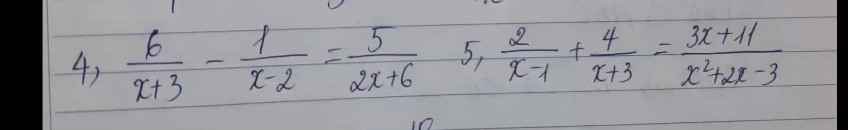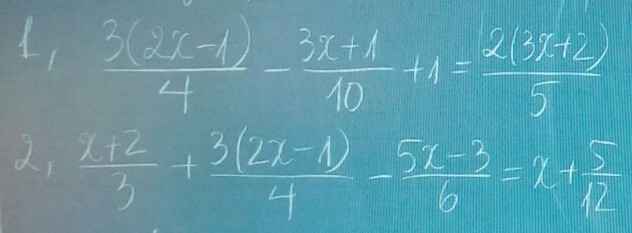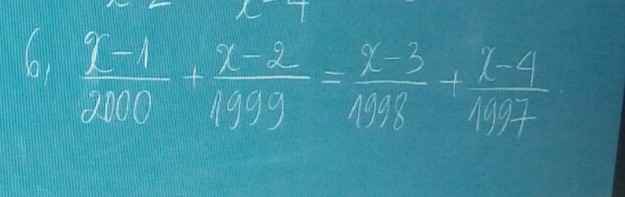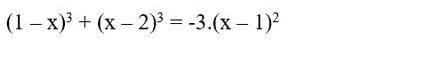đk : x khác 2 ; 4
<=> 5(x^2 - 7x + 12) - 5x^2 + 20x - 20 = 16( x - 2 )( x - 4 )
\(\Leftrightarrow-15x+40=16x^2-96x+128\Leftrightarrow16x^2-81x+88=0\Leftrightarrow x=\dfrac{-81\pm\sqrt{929}}{32}\)
\(\Leftrightarrow\dfrac{x^2-7x+12}{\left(x-2\right)\left(x-4\right)}-\dfrac{x^2-4}{\left(x-2\right)\left(x-4\right)}=\dfrac{16}{5}\)
\(\Leftrightarrow5\left(x^2-7x+12-x^2+4\right)=16\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow16x^2-96x+128=-35x+80\)
\(\Leftrightarrow16x^2-61x+48=0\)
Đến đây bạn chỉ cần giải phương trình bậc hai là xong
\(f,ĐKXĐ:\left\{{}\begin{matrix}x\ne2\\x\ne4\end{matrix}\right.\)
\(\dfrac{x-3}{x-2}-\dfrac{x-2}{x-4}=3\dfrac{1}{5}\\ \Leftrightarrow\dfrac{\left(x-3\right)\left(x-4\right)-\left(x-2\right)^2}{\left(x-2\right)\left(x-4\right)}=\dfrac{16}{5}\\ \Leftrightarrow\dfrac{x^2-7x+12-x^2+4x-4}{x^2-6x+8}=\dfrac{16}{5}\\ \Leftrightarrow\dfrac{-3x+8}{x^2-6x+8}=\dfrac{16}{5}\\ \Leftrightarrow5\left(-3x+8\right)=16\left(x^2-6x+8\right)\\ \Leftrightarrow-15x+40=16x^2-96x+128\)
\(\Leftrightarrow16x^2-96x+128+15x-40=0\\ \Leftrightarrow16x^2-81x+88=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{81+\sqrt{929}}{32}\left(tm\right)\\x=\dfrac{81-\sqrt{929}}{32}\left(tm\right)\end{matrix}\right.\)