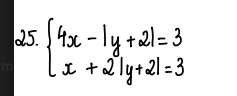\(\left\{{}\begin{matrix}4x-\left|y+2\right|=3\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-2\left|y+2\right|+x+2\left|y+2\right|=6+3\\\left|y+2\right|=4x-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x=9\\\left|y+2\right|=4x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\left|y+2\right|=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y+2\in\left\{1;-1\right\}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y\in\left\{-1;-3\right\}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}4x-\left|y+2\right|=3\\x+2\left|y+2\right|=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x-\left|y+2\right|=3\\4x+8\left|y+2\right|=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2\left|y+2\right|=3\\\left|y+2\right|=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2.\dfrac{5}{3}=3\\\left|y+2\right|=\dfrac{5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\\left|y+2\right|=\dfrac{5}{3}\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}y+2=\dfrac{5}{3}\\y+2=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}y=-\dfrac{1}{3}\\y=-\dfrac{11}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình đã cho là
\(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=-\dfrac{1}{3}\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=-\dfrac{11}{3}\end{matrix}\right.\)