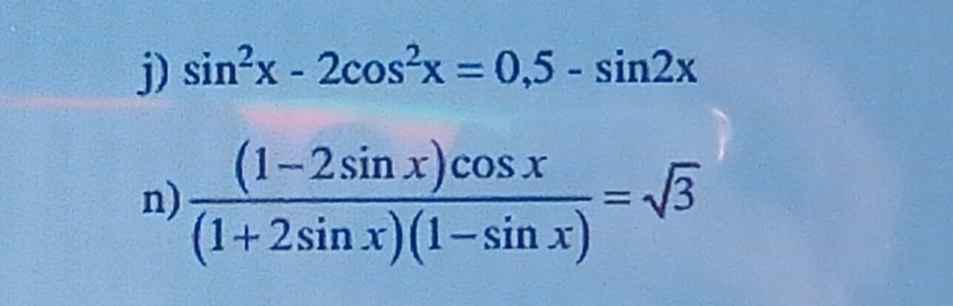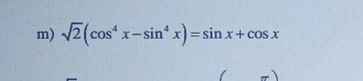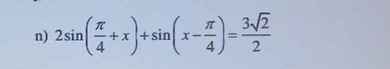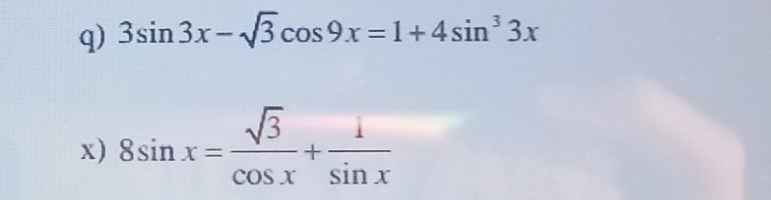j)\(sin^2x-2cos^2x=0,5-sin2x\)
\(\Leftrightarrow sin^2x-2cos^2x=\dfrac{1}{2}\left(sin^2x+cos^2x\right)-2.sinx.cosx\)
\(\Leftrightarrow\dfrac{1}{2}sin^2x+2.sinx.cosx-\dfrac{5}{2}cos^2x=0\)
\(\Leftrightarrow\dfrac{1}{2}\left(sinx-cosx\right)\left(sinx+5cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\left(1\right)\\sinx+5cosx=0\left(2\right)\end{matrix}\right.\)
Từ (1)\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Từ (2)\(\Leftrightarrow sinx=-5cosx\)
Xét \(cosx=0\Rightarrow\left\{{}\begin{matrix}sinx=1\\sin2x=0\end{matrix}\right.\) thay vào pt ban đầu thấy ktm
=>\(cosx\ne0\)
Pt (2)\(\Leftrightarrow\dfrac{sinx}{cosx}=-5\Leftrightarrow tanx=-5\)
\(\Leftrightarrow x=arctan\left(-5\right)+k\pi\) (\(k\in Z\))
Vậy...
n) Đk:\(x\ne\dfrac{-\pi}{6}+k2\pi;x\ne\dfrac{7\pi}{6}+k2\pi;x\ne\dfrac{\pi}{2}+k2\pi\) (\(k\in Z\))
PT \(\Rightarrow\left(1-2.sinx\right)cosx=\sqrt{3}\left(1+2sinx\right)\left(1-sinx\right)\)
\(\Leftrightarrow cosx-2.sinx.cosx=\sqrt{3}\left(1+sinx-2sin^2x\right)\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(cos^2x+sin^2x+sinx-2sin^2x\right)\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(cos^2x-sin^2x+sinx\right)\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(cos2x+sinx\right)\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x+\sqrt{3}cos2x\)
\(\Leftrightarrow2.cos\left(x+\dfrac{\pi}{3}\right)=2.cos\left(2x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}-k2\pi\\x=\dfrac{-\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\) (k nguyên)
Kết hợp với đk => \(x=-\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\) (k nguyên)