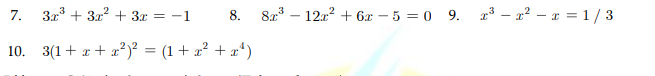7: \(3x^3+3x^2+3x=-1\)
=>\(3x^3+3x^2+3x+1=0\)
=>\(x\simeq-0,44\)
8: \(8x^3-12x^2+6x-5=0\)
=>\(8x^3-12x^2+6x-1-4=0\)
=>\(\left(2x-1\right)^3=4\)
=>\(2x-1=\sqrt[3]{4}\)
=>\(2x=\sqrt[3]{4}+1\)
=>\(x=\dfrac{\sqrt[3]{4}+1}{2}\)
9: \(x^3-x^2-x=\dfrac{1}{3}\)
=>\(3x^3-3x^2-3x=1\)
=>\(3x^3-3x^2-3x-1=0\)
=>\(x\simeq1,702\)
10: \(3\left(1+x+x^2\right)^2=1+x^2+x^4\)
=>\(3\left(x^2+x+1\right)^2=x^4+2x^2+1-x^2\)
=>\(3\left(x^2+x+1\right)^2=\left(x^2+1\right)^2-x^2\)
=>\(3\left(x^2+x+1\right)^2=\left(x^2+x+1\right)\left(x^2-x+1\right)\)
=>\(\left(x^2+x+1\right)\left(3x^2+3x+3-x^2+x-1\right)=0\)
=>\(\left(x^2+x+1\right)\left(2x^2+4x+2\right)=0\)
=>\(2\left(x^2+x+1\right)\left(x^2+2x+1\right)=0\)
mà \(2>0;x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
nên \(x^2+2x+1=0\)
=>\(\left(x+1\right)^2=0\)
=>x+1=0
=>x=-1