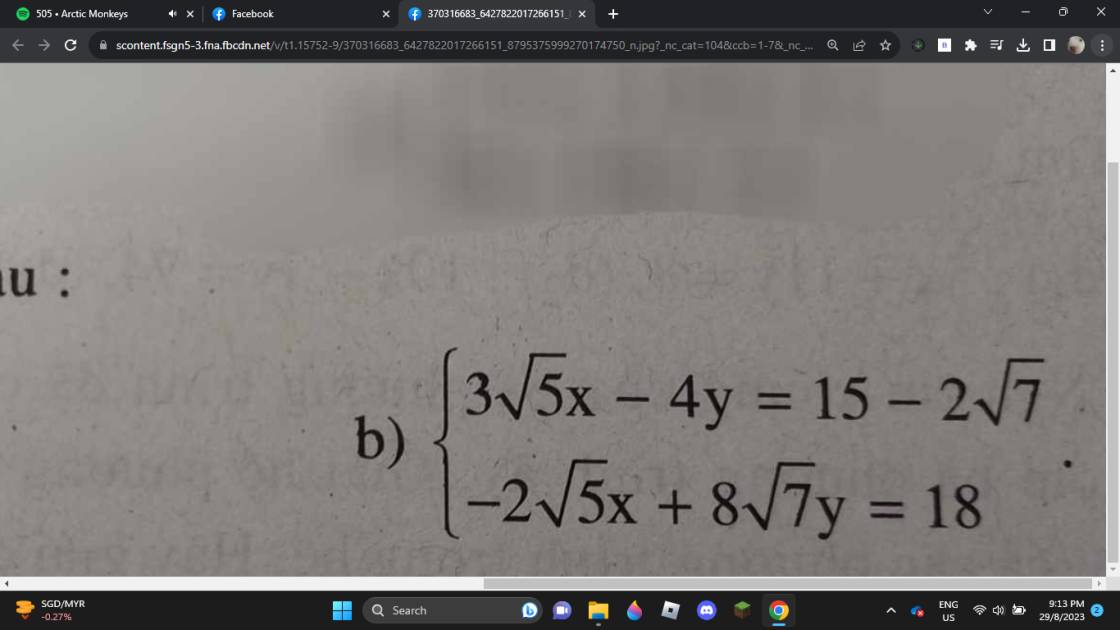
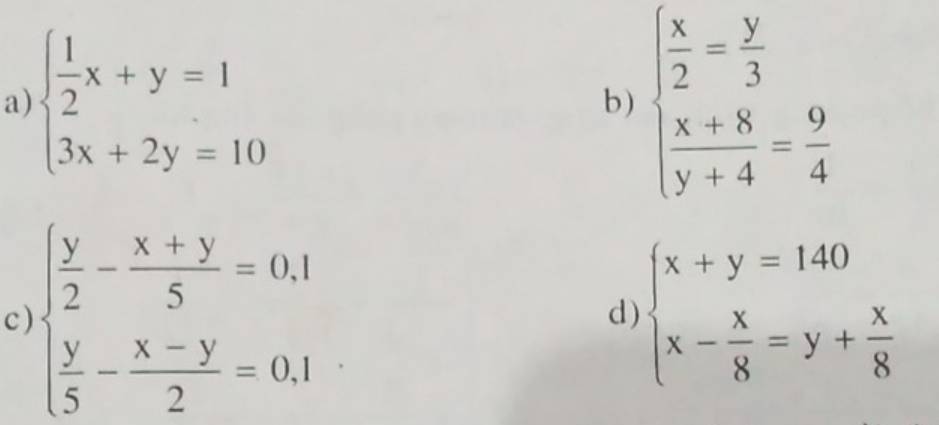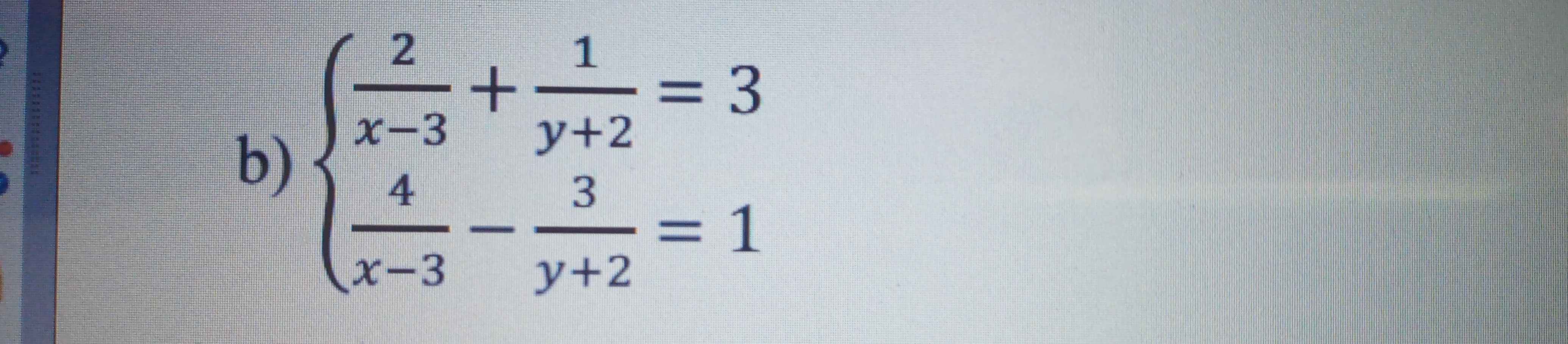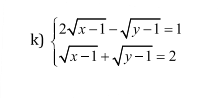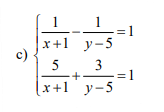a: \(\left\{{}\begin{matrix}\dfrac{1}{2}x+y=1\\3x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=2\\3x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-8\\x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\2y=2-x=2-4=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=-1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{x+8}{y+4}=\dfrac{9}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=2y\\4\left(x+8\right)=9\left(y+4\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=0\\4x-9y=36-32=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-8y=0\\12x-27y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-12\\3x-2y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{12}{19}\\3x=2y=2\cdot\dfrac{-12}{19}=-\dfrac{24}{19}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{8}{19}\\y=-\dfrac{12}{19}\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{y}{2}-\dfrac{x+y}{5}=0,1\\\dfrac{y}{5}-\dfrac{x-y}{2}=0,1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5y-2\left(x+y\right)}{10}=\dfrac{1}{10}\\\dfrac{2y-5\left(x-y\right)}{10}=\dfrac{1}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5y-2x-2y=1\\2y-5x+5y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+3y=1\\-5x+7y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-10x+15y=5\\-10x+14y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\2x-3y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\2x=3y-1=3\cdot3-1=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}x+y=140\\x-\dfrac{x}{8}=y+\dfrac{x}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=140\\\dfrac{3}{4}x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{4}x=140\\x+y=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=140:\dfrac{7}{4}=140\cdot\dfrac{4}{7}=80\\y=140-80=60\end{matrix}\right.\)