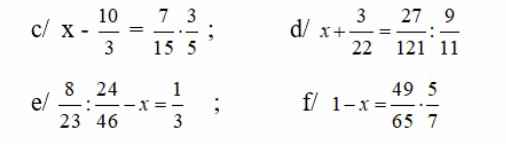a; (\(x^3\) - \(x^2\)y) - (\(x^2\) - y2)
= \(x^2\).(\(x-y\)) - (\(x-y\)).(\(x+y\))
= (\(x-y\)).(\(x^2\) - \(x-y\))
b; 3(\(x-y\)) + ay - a\(x\)
= 3(\(x-y\)) - a(\(x-y\))
= (\(x-y\))(3 - a)
a: \(x^3-x^2y-x^2+y^2\)
\(=x^2\left(x-y\right)-\left(x^2-y^2\right)\)
\(=x^2\left(x-y\right)-\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2-x-y\right)\)
b: \(3\left(x-y\right)+ay-ax\)
\(=3\left(x-y\right)-a\left(x-y\right)\)
=(x-y)(3-a)

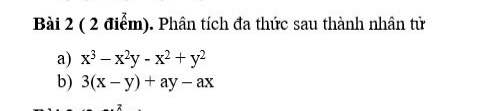










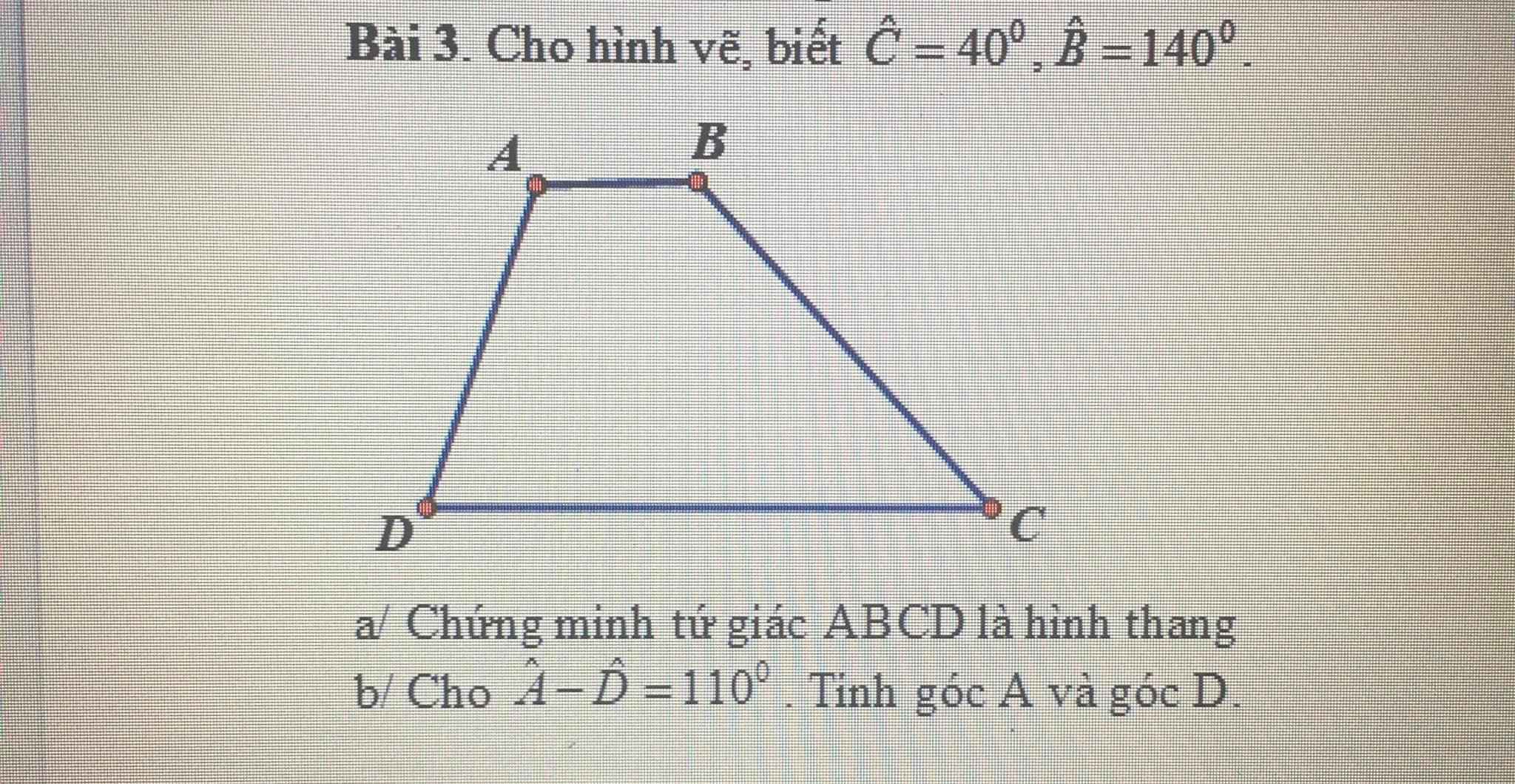





 ai giải giúp mình với ạ mình cảm ơn
ai giải giúp mình với ạ mình cảm ơn