\(a//b//c\)
\(=>\angle\left(A1\right)+\angle\left(B2\right)=180^o\)(2 góc ở vị trí trong cùng phía)
\(=>\angle\left(B2\right)=180^0-140^0=40^o\)
có \(\angle\left(B3\right)+\angle\left(B2\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B3\right)=180^0-40^0=140^o\)
b, \(\angle\left(B2\right)+\angle\left(B1\right)=180^o\left(ke-bu\right)\)
\(=>\angle\left(B1\right)=180^o-40^o=140^o\)
\(b//c=>\angle\left(B1\right)=\angle\left(C1\right)=140^o\)(2 góc đồng vị)
\(=>\angle\left(C4\right)+\angle\left(C1\right)=180^o\left(ke-bu\right)=>\angle\left(C4\right)=180^o-140^0=40^o\)
Giải:
Ta có: a//b//ca//b//c
=>∠(A1)+∠(B2)=180o=>∠(A1)+∠(B2)=180o(2 góc ở vị trí trong cùng phía)
=>∠(B2)=1800−1400=40o=>∠(B2)=1800−1400=40o
có ∠(B3)+∠(B2)=180o(ke−bu)∠(B3)+∠(B2)=180o(ke−bu)
=>∠(B3)=1800−400=140o=>∠(B3)=1800−400=140o
b, ∠(B2)+∠(B1)=180o(ke−bu)∠(B2)+∠(B1)=180o(ke−bu)
=>∠(B1)=180o−40o=140o=>∠(B1)=180o−40o=140o
b//c=>∠(B1)=∠(C1)=140ob//c=>∠(B1)=∠(C1)=140o(2 góc đồng vị)
=>∠(C4)+∠(C1)=180o(ke−bu)=>∠(C4)=180o−1400=40o
Giải:
Ta có: a//b//ca//b//c
=>∠(A1)+∠(B2)=180o=>∠(A1)+∠(B2)=180o(2 góc ở vị trí trong cùng phía)
=>∠(B2)=1800−1400=40o=>∠(B2)=1800−1400=40o
có ∠(B3)+∠(B2)=180o(ke−bu)∠(B3)+∠(B2)=180o(ke−bu)
=>∠(B3)=1800−400=140o=>∠(B3)=1800−400=140o
b, ∠(B2)+∠(B1)=180o(ke−bu)∠(B2)+∠(B1)=180o(ke−bu)
=>∠(B1)=180o−40o=140o=>∠(B1)=180o−40o=140o
b//c=>∠(B1)=∠(C1)=140ob//c=>∠(B1)=∠(C1)=140o(2 góc đồng vị)
=>∠(C4)+∠(C1)=180o(ke−bu)=>∠(C4)=180o−1400=40o
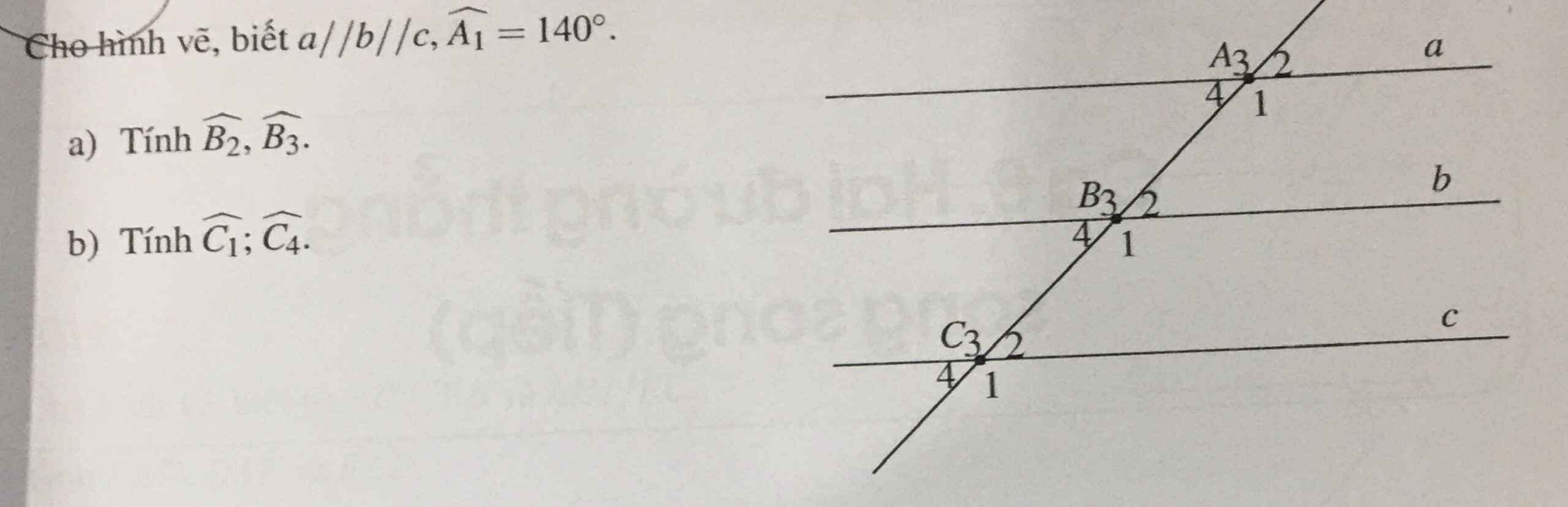
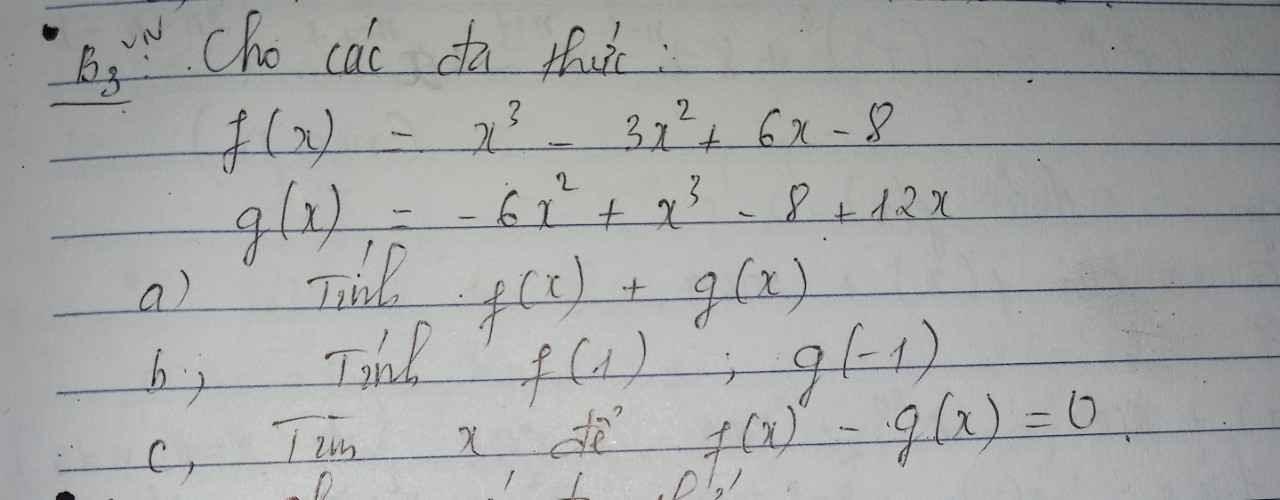
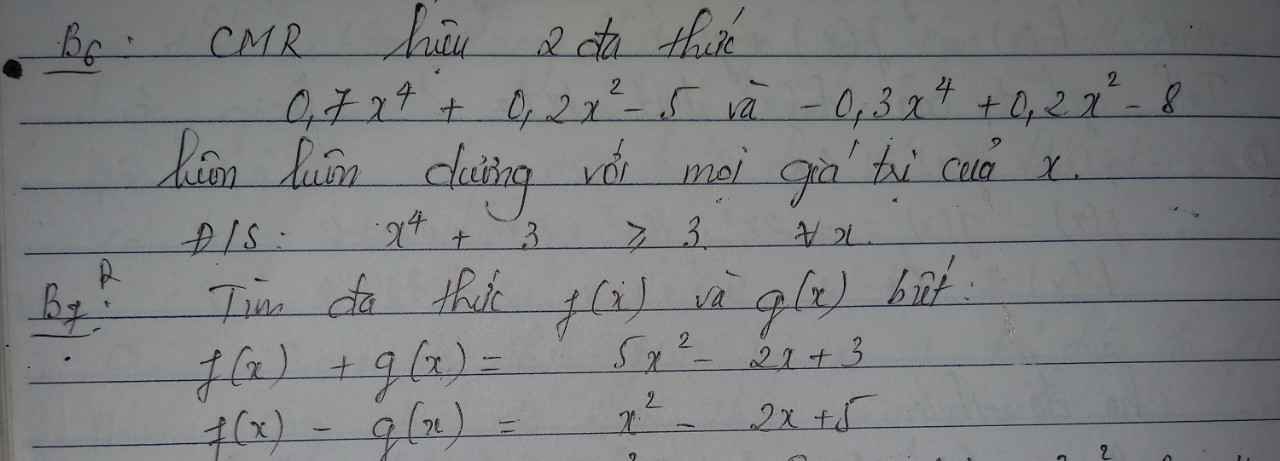
Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước