\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{16}{x^2-4}\)
\(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{16}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\left(x+2-x+2\right)\left(x+2+x-2\right)=16\)
\(\Leftrightarrow4\cdot2x=16\)
\(\Rightarrow x=2\)
\(--------\)
\(\dfrac{x+3}{x-2}+\dfrac{x+2}{x-3}=2\)
\(\Leftrightarrow\dfrac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}=\dfrac{2\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\)
\(\Leftrightarrow x^2-9+x^2-4=2x^2-10x+12\)
\(\Leftrightarrow2x^2-13=2x^2-10x+12\)
\(\Leftrightarrow-10x+12=-13\)
\(\Rightarrow x=2,5\)
#NgTienDat
\(\dfrac{1}{x+1}-\dfrac{x}{x^2-x+1}=\dfrac{3x}{x^3+1}\left(x\ne-1\right)\\ \Leftrightarrow\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{3x}{\left(x+1\right)\left(x^2-x+1\right)}\\ \Leftrightarrow x^2-x+1-x\left(x+1\right)=3x\\ \Leftrightarrow x^2-x+1-x^2-x=3x\\ \Leftrightarrow-2x+1=3x\\ \Leftrightarrow2x+3x=1\\ \Leftrightarrow5x=1\\ \Leftrightarrow x=\dfrac{1}{5}\left(tm\right)\)
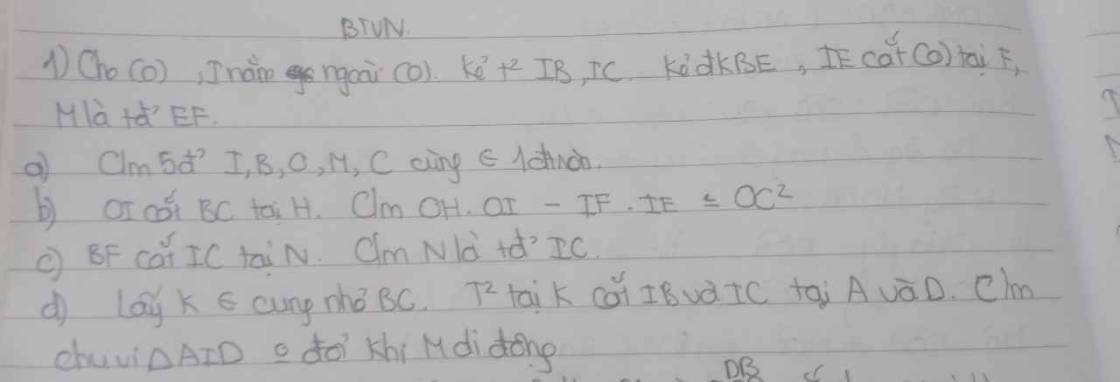
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
