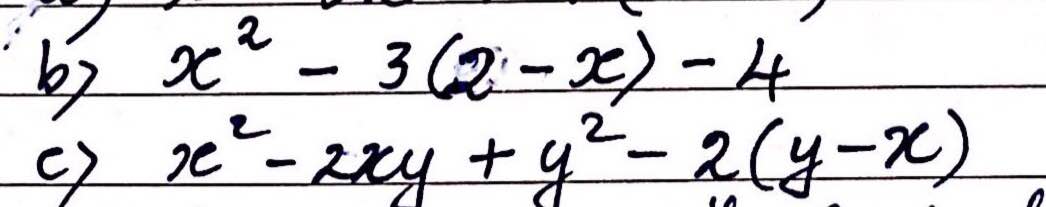Question

Giải giúp em hai câu này với ah

Answer 1

b: \(=x^2-6+3x-4=x^2+3x-10=\left(x+5\right)\left(x-2\right)\)

c: \(=\left(x-y\right)^2+2\left(x-y\right)=\left(x-y\right)\left(x-y+2\right)\)

Answer 2

\(b,=x^2-6+3x-4\\ =x^2-3x-10=x^2-5x+2x-10=x\left(x-5\right)+2\left(x-5\right)=\left(x+2\right)\left(x-5\right)\\ c,=\left(x-y\right)^2+2\left(x-y\right)=\left(x-y\right)\left(x-y+2\right)\)

Answer 3

b.x\(^2\)-6+3x-4

<=>(x\(^2\)+3x)+(-6-4)

<=>x(x+3)-10

<=>(x-10)(x+3)

<=>\(\left[{}\begin{matrix}x=10\\x=-3\end{matrix}\right.\)

Answer 4

b)=  \(x^2-(6-3x)-4\)
=\(x^2-6+3x-4\)
=\(x^2+(-6-4)+3x\)
=\(x^2-10+3x\)

 

Answer 5

b)= x²- (6 - 3x) -4

= x²- 6 +3x - 4

= x² + 3x - 10

= x² - 5x + 2x - 10

= (x² - 5x) + (2x - 10)

= x(x - 5) + 2(x - 5)

= (x+2) (x - 5)

c) = (x - y)² + 2(x - y) = (x - y) (x - y + 2)