1:Ta có: ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Ta có: \(\widehat{OIA}=\widehat{OBA}=\widehat{OCA}=90^0\)
=>O,I,B,A,C cùng thuộc đường tròn đường kính OA
2: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
ta có: HB=HC
=>H nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra O,H,A thẳng hàng
Vì AO là đường trung trực của BC
và AO cắt BC tại H
nên AO\(\perp\)BC tại H
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OE(=R)
nên \(OH\cdot OA=OE^2\)
Xét ΔOIA vuông tại I và ΔOHS vuông tại H có
\(\widehat{IOA}\) chung
Do đó: ΔOIA~ΔOHS
=>\(\dfrac{OI}{OH}=\dfrac{OA}{OS}\)
=>\(OI\cdot OS=OH\cdot OA\)
=>\(OI\cdot OS=OE^2\)
mà OE=OF
nên \(OI\cdot OS=OF^2\)
=>\(\dfrac{OI}{OF}=\dfrac{OF}{OS}\)
Xét ΔOIF và ΔOFS có
\(\dfrac{OI}{OF}=\dfrac{OF}{OS}\)
\(\widehat{IOF}\) chung
Do đó: ΔOIF~ΔOFS
=>\(\widehat{OIF}=\widehat{OFS}\)
=>\(\widehat{OFS}=90^0\)
=>SF là tiếp tuyến của (O)
a.
Do AB, AC là tiếp tuyến \(\Rightarrow\widehat{OBA}=\widehat{OCA}=90^0\)
Theo giả thiết \(OI\perp EF\Rightarrow\widehat{OIA}=90^0\)
3 điểm I, B, C cùng nhìn OA dưới 1 góc vuông nên 5 điểm A, B, I, O, C cùng thuộc đường tròn đường kính OA
b.
Do H là trung điểm BC \(\Rightarrow OH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông OAB với đường cao BH:
\(OB^2=OH.OA\Rightarrow OE^2=OH.OA\) (do \(OE=OB=R\))
\(\Rightarrow\dfrac{OE}{OA}=\dfrac{OH}{OE}\Rightarrow\Delta OHE\sim\Delta OEA\left(c.g.c\right)\)
\(\Rightarrow\widehat{OEH}=\widehat{OAE}\)
Mà \(\widehat{OAE}=\widehat{OSH}\) (cùng phụ \(\widehat{SOA}\))
\(\Rightarrow\widehat{OEH}=\widehat{OSH}\)
\(\Rightarrow OHES\) nội tiếp
\(\Rightarrow\widehat{SEO}=\widehat{SHO}=90^0\)
Mặt khác \(\left\{{}\begin{matrix}OI\perp EF\\OE=OF=R\end{matrix}\right.\) \(\Rightarrow OI\) hay OS là trung trực của EF
\(\Rightarrow\widehat{SFO}=\widehat{SEO}=90^0\)
Hay \(SF\perp OF\Rightarrow SF\) là tiếp tuyến của (O)
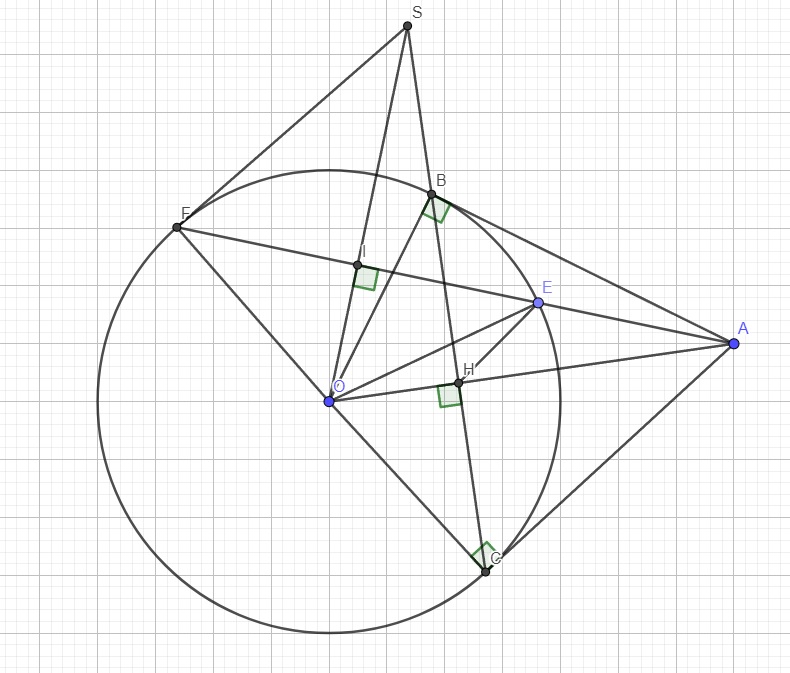
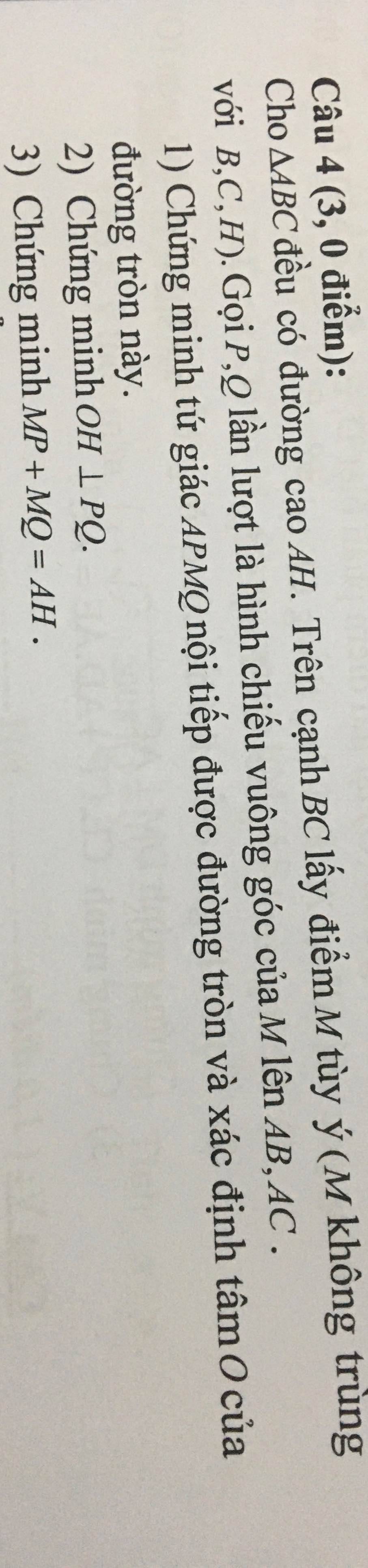
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
