a: Xét tứ giác APMQ có \(\widehat{APM}+\widehat{AQM}=90^0+90^0=180^0\)
nên APMQ là tứ giác nội tiếp đường tròn đường kính AM
Tâm O là trung điểm của AM
b: Ta có: ΔAHM vuông tại H
=>H nằm trên đường tròn đường kính AM
=>H nằm trên (O)
Ta có: ΔABC đều
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét (O) có
\(\widehat{PAH}\) là góc nội tiếp chắn cung PH
\(\widehat{QAH}\) là góc nội tiếp chắn cung QH
\(\widehat{PAH}=\widehat{QAH}\left(cmt\right)\)
Do đó: \(sđ\stackrel\frown{HP}=sđ\stackrel\frown{HQ}\)
Xét (O) có
\(\widehat{QPH}\) là góc nội tiếp chắn cung QH
\(\widehat{HQP}\) là góc nội tiếp chắn cung HP
\(sđ\stackrel\frown{QH}=sđ\stackrel\frown{HP}\)
Do đó: \(\widehat{HPQ}=\widehat{HQP}\)
=>HQ=HP
=>H nằm trên đường trung trực của QP(1)
Ta có: OP=OQ
=>O nằm trên đường trung trực của QP(2)
Từ (1) và (2) suy ra HO là đường trung trực của PQ
=>HO\(\perp\)PQ

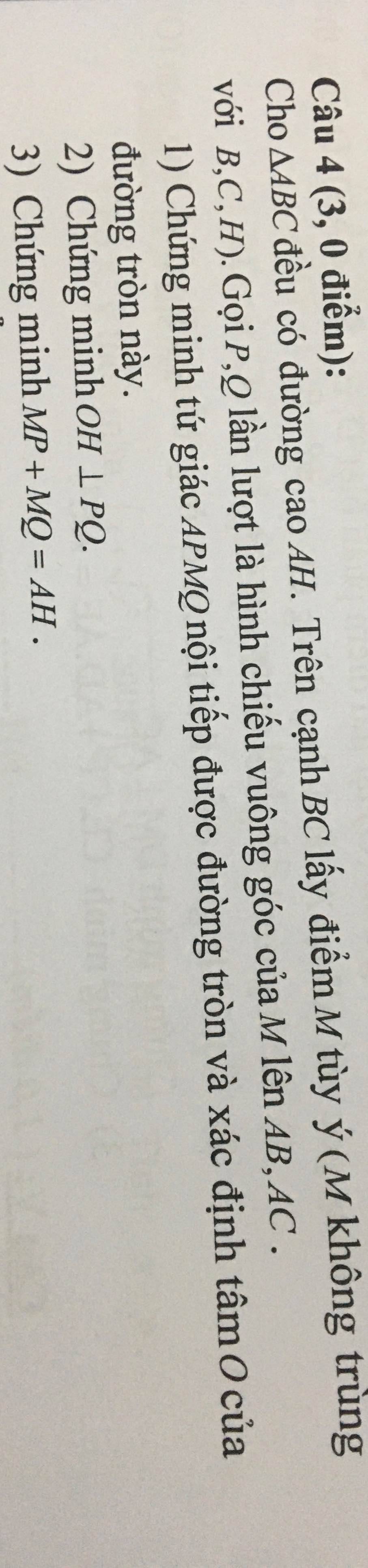














 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn

