Bài 6:
a: Xét ΔADB vuông tại D và ΔADC vuông tại D có
AB=AC
AD chung
Do đó: ΔADB=ΔADC
=>DB=DC
b: Ta có: ΔADB=ΔADC
=>\(\widehat{BAD}=\widehat{CAD}\)
Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔAHD=ΔAKD
=>DH=DK
c: Ta có: ΔAHD=ΔAKD
=>AH=AK
Xét ΔABC có \(\dfrac{AH}{AB}=\dfrac{AK}{AC}\)
nên HK//BC
Bài 5:
a: Xét ΔADB và ΔAEC có
AD=AE
\(\widehat{DAB}\) chung
AB=AC
Do đó: ΔADB=ΔAEC
b: Ta có: AE+EB=AB
AD+DC=AC
mà AE=AD và AB=AC
nên EB=DC
Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=DB(ΔABD=ΔACE)
Do đó; ΔEBC=ΔDCB
=>\(\widehat{ECB}=\widehat{DBC}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên ED//BC








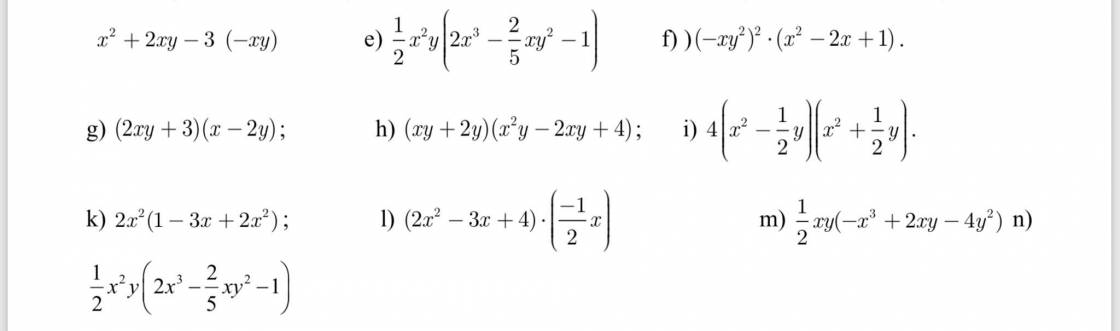
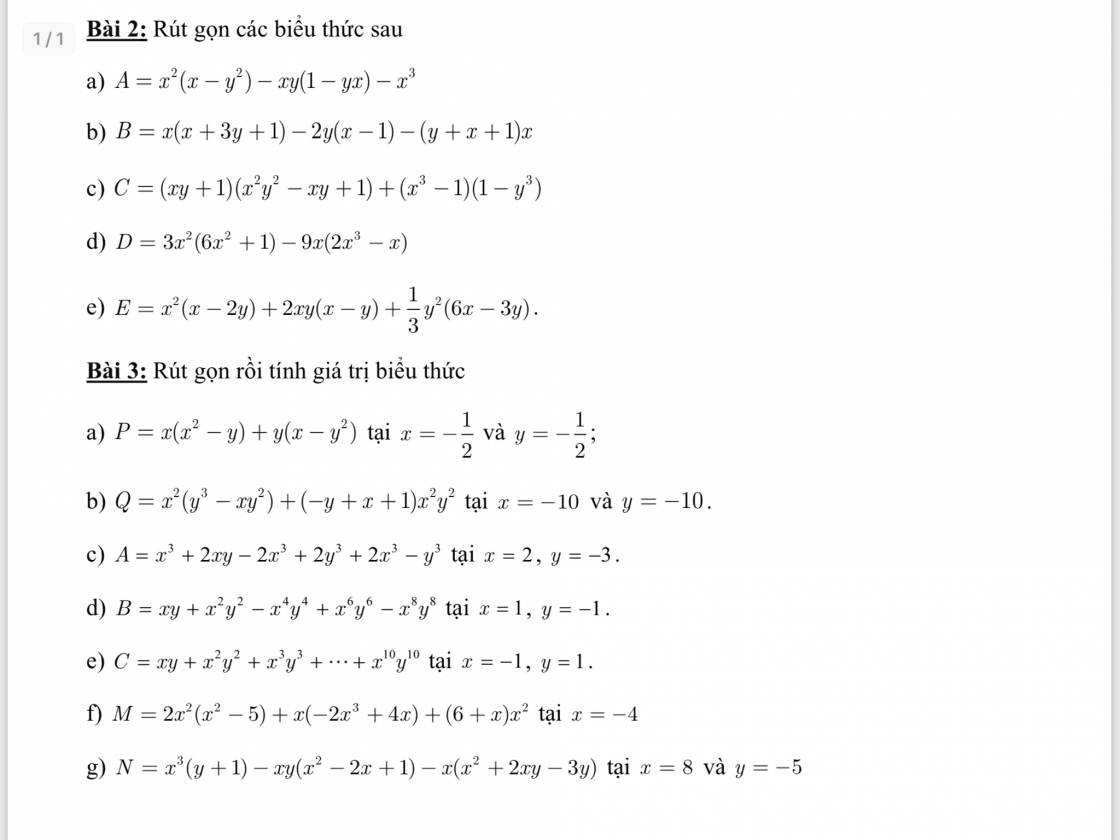














 các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II