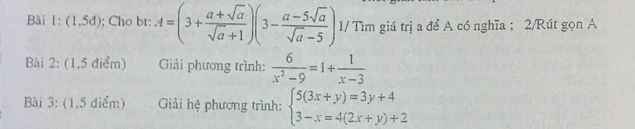Bài 2: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\Leftrightarrow\dfrac{6}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2-9+x+3}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
=>x=-4(nhận) hoặc x=3(loại)
Bài 1:
a,ĐKXĐ:\(\left\{{}\begin{matrix}\sqrt{a}+1\ne0\left(luôn.đúng\right)\\\sqrt{a}-5\ne0\end{matrix}\right.\Leftrightarrow\sqrt{a}\ne5\Leftrightarrow a\ne25\)
\(b,A=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-5\sqrt{a}}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-5\right)}{\sqrt{a}-5}\right)\)
\(\Rightarrow A=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)\)
\(\Rightarrow A=9-a\)