\(a,\left[6.\left(-\dfrac{1}{3}\right)^2-3.\left(-\dfrac{1}{3}\right)+1\right]:\left(-\dfrac{1}{3}-1\right)\)
\(=\left[6.\dfrac{1}{9}-\dfrac{1.\left(-1\right)}{1}+1\right]:\left(-\dfrac{1}{3}-\dfrac{3}{3}\right)\)
\(=\left[\dfrac{2.1}{3}-\left(-1\right)+1\right]:\dfrac{-4}{3}\)
\(=\left[\dfrac{2}{3}+1+1\right].\dfrac{-3}{4}\)
\(=\left[\dfrac{2}{3}+\dfrac{3}{3}+\dfrac{3}{3}\right].\dfrac{-3}{4}\)
\(=\dfrac{8}{3}.\dfrac{-3}{4}\)
\(=\dfrac{2.\left(-1\right)}{1.1}\)
\(=-2\)
\(b,\dfrac{\left(\dfrac{2}{3}\right)^3.\left(-\dfrac{3}{4}\right)^2.\left(-1\right)^{2003}}{\left(\dfrac{2}{5}\right)^2.\left(-\dfrac{5}{12}\right)^3}\)
\(=\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{3}{4}\right)^2.\left(-1\right)}{\left(\dfrac{2}{5}\right)^2.\left(-\dfrac{5}{12}\right)^3}\)
\(=\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{3}{4}\right)^2}{\left(\dfrac{2}{5}\right)^2\left(\dfrac{5}{12}\right)^3}\)
\(=\dfrac{\dfrac{2^3}{3^3}.\dfrac{3^2}{4^2}}{\dfrac{2^2}{5^2}.\dfrac{5^3}{12^3}}\)
\(=\dfrac{\dfrac{2^3.3^2}{3^3.4^2}}{\dfrac{2^2.5^3}{5^2.12^3}}\)
\(=\dfrac{2^3.3^2.5^2.12^3}{3^3.4^2.2^2.5^3}\)
\(=\dfrac{2^3.3^2.5^2.\left(4.3\right)^3}{3^3.2^4.2^2.5^3}\)
\(=\dfrac{2^3.3^2.5^2.4^3.3^3}{3^3.2^6.5^3}\)
\(=\dfrac{2^3.3^2.5^2.\left(2^2\right)^3.3^3}{3^3.2^6.5^3}\)
\(=\dfrac{2^3.3^2.5^2.2^6.3^3}{3^3.2^6.5^3}\)
\(=\dfrac{2^9.3^5.5^2}{3^3.2^6.5^3}\)
\(=\dfrac{2^3.3^2}{5}\)
\(=\dfrac{8.9}{5}\)
\(=\dfrac{72}{5}\)
Đúng 5
Bình luận (1)
Các câu hỏi tương tự
giải chi tiết hộ nha
Đọc tiếp
giải chi tiết hộ nha
giải chi tiết nha mn
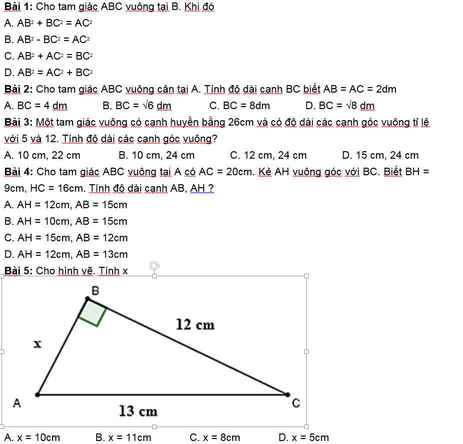
 Giải hộ chi tiết nha
Giải hộ chi tiết nha
 Giải chi tiết hộ mình nha!!!
Giải chi tiết hộ mình nha!!!
/x-2/+/3-2x/=2x+1, tìm x
các bạn giải chi tiết nha, chi tiết mình mới tick
Giúp mk với (lời giải chi tiết nha)

Giải chi tiết giúp mik câu b nha. Thankss
So sánh 227 và 318? Giải chi tiết giúp nha![]()
So sánh:
815 và 164
Giải chi tiết giúp mik nha.
So sánh:
\(2^{20}và3^{12}\)
Giải chi tiết giúp mik nha.














