a: \(\dfrac{1}{99}+\dfrac{2}{98}+...+\dfrac{99}{1}\)
\(=\left(\dfrac{1}{99}+1\right)+\left(\dfrac{2}{98}+1\right)+...+\left(\dfrac{98}{2}+1\right)+1\)
\(=\dfrac{100}{99}+\dfrac{100}{98}+...+\dfrac{100}{2}+\dfrac{100}{100}\)
\(=100\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)\)
\(\left(x+5\right)\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\left(\dfrac{1}{99}+\dfrac{2}{98}+...+\dfrac{99}{1}\right)\cdot\dfrac{1}{25}\)
=>\(\left(x+5\right)\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=100\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)\cdot\dfrac{1}{25}\)
=>x+5=4
=>x=-1
b:\(\dfrac{6}{2\cdot5}+\dfrac{10}{5\cdot10}+...+\dfrac{18}{n\left(n+9\right)}=-1\)
=>\(2\left(\dfrac{3}{2\cdot5}+\dfrac{5}{5\cdot10}+...+\dfrac{9}{n\left(n+9\right)}\right)=-1\)
=>\(2\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+...+\dfrac{1}{n}-\dfrac{1}{n+9}\right)=-1\)
=>\(2\left(\dfrac{1}{2}-\dfrac{1}{n+9}\right)=-1\)
=>\(1-\dfrac{2}{n+9}=-1\)
=>\(\dfrac{2}{n+9}=2\)
=>n+9=1
=>n=-8
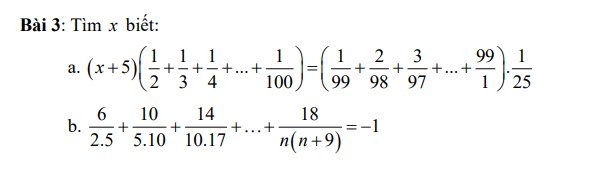
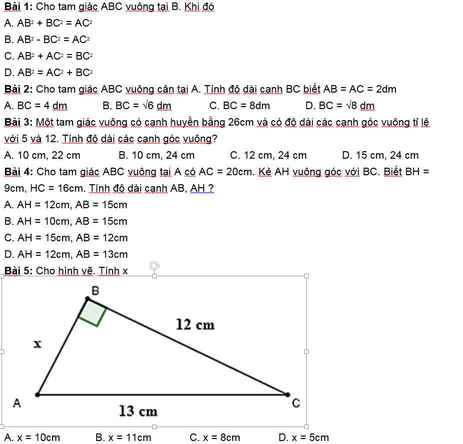
Giải chi tiết hộ mình nha!!!
