\(a,\dfrac{x+14}{86}+\dfrac{x+15}{85}+\dfrac{x+16}{84}+\dfrac{x+17}{83}+\dfrac{x+116}{4}=0\\ =>\left(\dfrac{x+14}{86}+1\right)+\left(\dfrac{x+15}{85}+1\right)+\left(\dfrac{x+16}{84}+1\right)+\left(\dfrac{x+17}{83}+1\right)+\left(\dfrac{x+116}{4}-4\right)=0\\ =>\dfrac{x+100}{86}+\dfrac{x+100}{85}+\dfrac{x+100}{84}+\dfrac{x+100}{83}+\dfrac{x+100}{4}=0\\ =>\left(x+100\right)\left(\dfrac{1}{86}+\dfrac{1}{85}+\dfrac{1}{84}+\dfrac{1}{83}+\dfrac{1}{4}\right)=0\\ =>x+100=0\\ =>x=-100\\ b,\dfrac{x-90}{10}+\dfrac{x-76}{12}+\dfrac{x-58}{14}+\dfrac{x-36}{16}+\dfrac{x-15}{17}=15\\ =>\left(\dfrac{x-90}{10}-1\right)+\left(\dfrac{x-76}{12}-2\right)+\left(\dfrac{x-58}{14}-3\right)+\left(\dfrac{x-36}{16}-4\right)+\left(\dfrac{x-15}{17}-5\right)=0\)
\(=>\dfrac{x-100}{10}+\dfrac{x-100}{12}+\dfrac{x-100}{14}+\dfrac{x-100}{16}+\dfrac{x-100}{17}=0\\ =>\left(x-100\right)\left(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}\right)=0\\ =>x-100=0\\ =>x=100\)
\(c,\dfrac{2-x}{2020}-1=\dfrac{1-x}{2021}-\dfrac{x}{2022}\\ =>\dfrac{x-2}{2020}+1=\dfrac{x-1}{2021}+\dfrac{x}{2022}\\ =>\dfrac{x-2}{2020}-1=\left(\dfrac{x-1}{2021}-1\right)+\left(\dfrac{x}{2022}-1\right)\\ =>\dfrac{x-2022}{2020}=\dfrac{x-2022}{2021}+\dfrac{x-2022}{2022}\\ =>\dfrac{x-2022}{2020}-\dfrac{x-2022}{2021}-\dfrac{x-2022}{2022}=0\\ =>\left(x-2022\right)\left(\dfrac{1}{2020}-\dfrac{1}{2021}-\dfrac{1}{2022}\right)=0\\ =>x-2022=0\\ =>x=2022\)
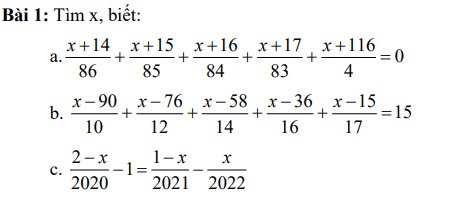
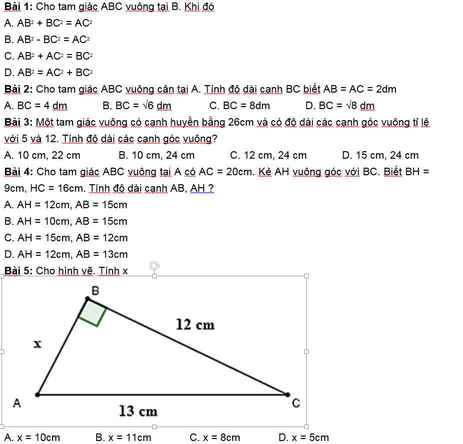
Giải chi tiết hộ mình nha!!!
