`15,`
`a,`
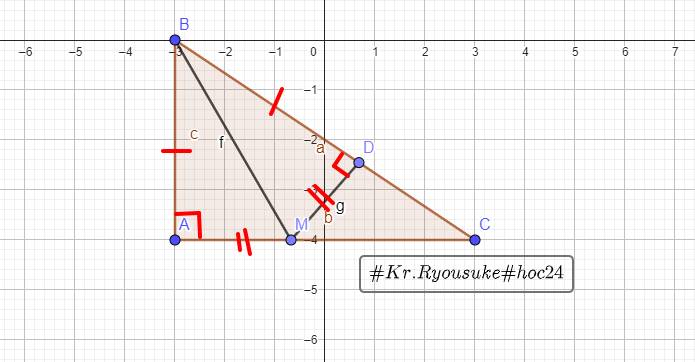
Xét `\Delta ABM` và `\Delta DBM`:
`\text {BA = BD (gt)}`
$\widehat {ABM} = \widehat {DBM} (\text {BM là tia phân giác}$ $\widehat {ABD})$
`\text {BM chung}`
`=> \Delta ABM = \Delta DBM (c-g-c)`
`b,`
Vì `\Delta ABM = \Delta DBM (a)`
`->` $\widehat {BAM} = \widehat {BDM} (\text {2 góc tương ứng})$
Mà `\hat {A} = 90^0`
`->` $\widehat {BAM} = \widehat {BDM} = 90^0`
`-> \text {MD} \bot \text {BC}`
`c,`
Vì `\Delta ABM = \Delta DBM (a)`
`-> \text {MA = MD (2 cạnh tương ứng)}` `(1)`
Xét `\Delta MDC`:
`\hat {D} = 90^0`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`-> \text {MC là cạnh lớn nhất}`
`-> \text {MC > MD}` `(2)`
Từ `(1)` và `(2)`
`-> \text {MC > MA}`.
`14,`
`a,`
`-` Rút ngẫu nhiên `1` thẻ trong hộp
`->` Số khả năng có thể xảy ra là `15`
`->` Số phần tử của tập hợp `B` là `15`
`b,`
`-` Các số `\vdots` cho `3` trong các số trên là `3; 6; 9; 12; 15`
`-` Các số có khả năng xuất hiện ở trên gồm `15` số
`->` Xác suất để rút được thẻ có số `\vdots` cho `3` là `5/15 = 1/3`
Sao bạn không post bài lên trên mà lại để bài ở phần bình luận? Như vậy,những người hay nhấn vào các câu hỏi "Chưa trả lời" sẽ thường bỏ qua bài của bạn?





