a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC
Suy ra: \(\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
hay \(AC^2=HC\cdot BC\)
c: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
Suy ra: \(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
hay \(AH^2=HB\cdot HC\)
d: Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{AH\cdot BC}{2}\)









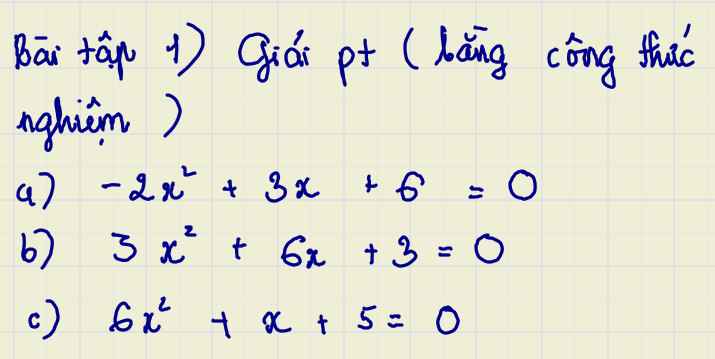

 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn





 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn