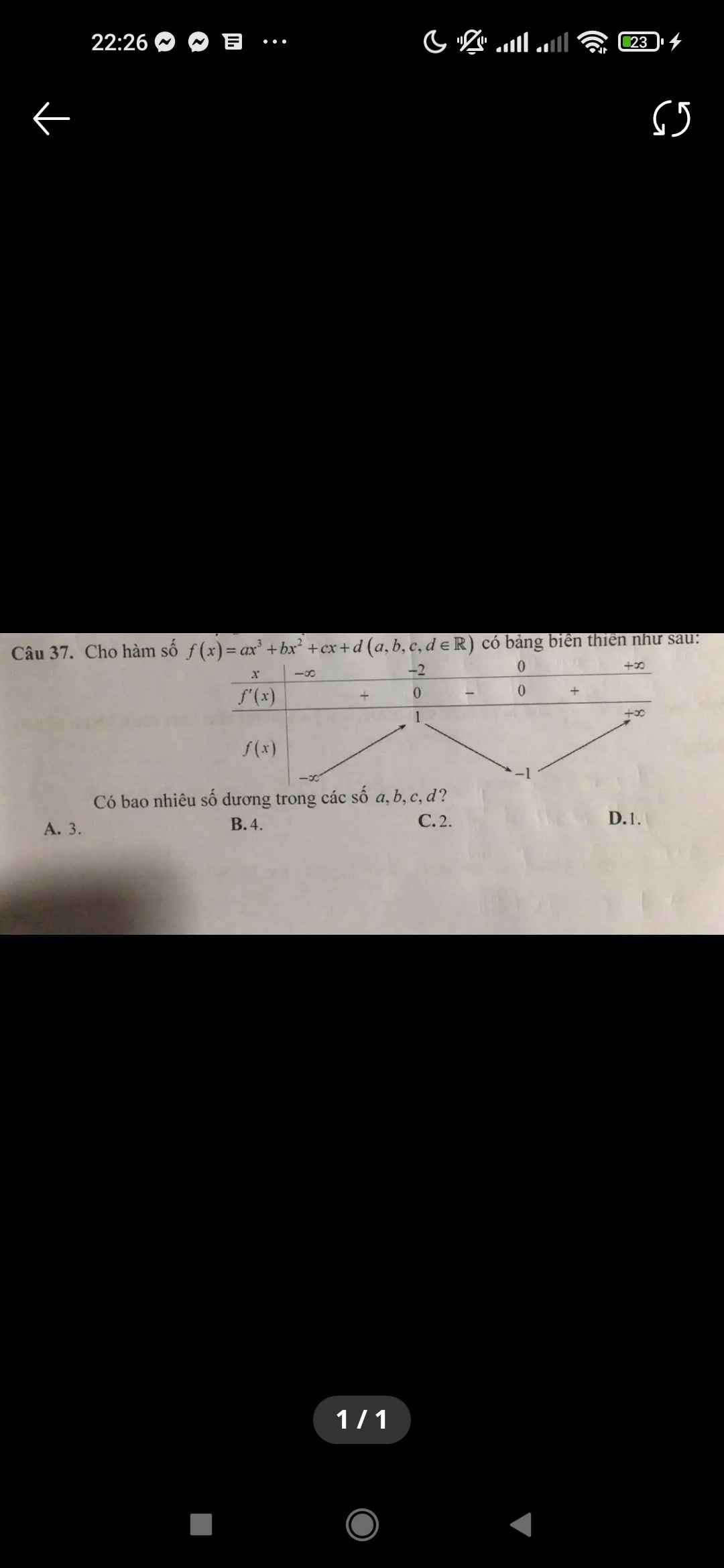
\(\lim\limits_{x\rightarrow+\infty}y=+\infty\Rightarrow a>0\)
\(x=0\Rightarrow y=d=-1< 0\)
\(y'=3ax^2+2bx+c=0\) có nghiệm \(x=0\Rightarrow c=0\)
Khi đó: \(y'=3ax^2+2bx=x\left(3ax+2b\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2b}{3a}\end{matrix}\right.\)
\(\Rightarrow-\dfrac{2b}{3a}=-2\Rightarrow b=3a>0\)
Vậy có 2 số dương là a và b
Giải chi tiết giúp e vs 
Tích phân của (-x²+x+2) cận từ -1 đến 2. Mọi người giải chi tiết giúp em với ạ. Em cảm ơn
GIÚP MÌNH GIẢI CHI TIẾT CÂU 57 - 60 VỚI Ạ 
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
Giải hôh em bài 4 với ạ em xin lời giải chi tiết
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc giữa CA’ và mặt (AA’B’B) bằng 30o. Thể tích khối lăng trụ ABC.A’B’C’ là?
Hãy giải chi tiết bài này giúp mình với ạ.
Trình bày tự luận chi tiết dẽ hiểu giúp em câu 1208 với ạ
Một hòm đựng 10 chi tiết chính phẩm và 5 chi tiết phế phẩm. Lấy đồng thời 3 chi tiết. Tính xác suất để được 2 chi tiết chính phẩm.
Cho hàm số: \(y=-x^3+3\left(m+1\right)x^2-\left(3m^2+7m-1\right)x+m^2-1.\)
Tìm giá trị thực của m để hàm số đạt cực tiểu tại một điểm có hoành độ nhỏ hơn 1.
Ai giải chi tiết giúp em với ạ.
Giúp e vs
