Với điều kiện x > 0, ta có phương trình
e 2 . e lnx = x + 3
⇔ e 2 .x = x + 3
⇔x( e 2 − 1) = 3
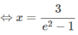
(thỏa mãn điều kiện)
Với điều kiện x > 0, ta có phương trình
e 2 . e lnx = x + 3
⇔ e 2 .x = x + 3
⇔x( e 2 − 1) = 3
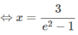
(thỏa mãn điều kiện)
Giải các phương trình sau:
a) e 2 + ln x = x + 3;
b) e 4 - ln x = x;
c) (5 − x).log(x − 3) = 0
Giải các phương trình sau: e 4 - lnx = x + 3
Giải các phương trình sau: ln(4x + 2) - ln(x - 1) = lnx
Giải các bất phương trình lôgarit sau: lnx + 2 lnx - 1 < 0
Giải phương trình lnx + ln(x - 1) = ln2
A. x = 3/2
B. x = -1, x = 2
C. x = 2
D. x = 1, x = 3/2
Cho các hàm số f 0 ( x ) , f 1 ( x ) , f 2 ( x ) , . . . thỏa mãn f 0 x = ln x + ln x - 2019 - ln x + 2019 , f n + 1 x = f n x - 1 , ∀ n ∈ ℕ . Số nghiệm của phương trình f 2020 x = 0 là
A. 6058
B. 6057
C. 6059
D. 6063
Giải phương trình ( x 2 - 2 x ) l n x = l n x 3
A. x = 1, x = 3
B. x = -1, x = 3
C. x = ±1, x = 3
D. x = 3
gọi S là tập hợp tất cả các giá trị m để phương trình m lnx - x lnm = x-m có 2 nghiệm phân biệt. tìm tập S
Giả sử x là nghiệm của phương trình 4 1 x - 2 = ln e 2 . Tính lnx
A. 0
B. ln3
C. -ln3
D. 1