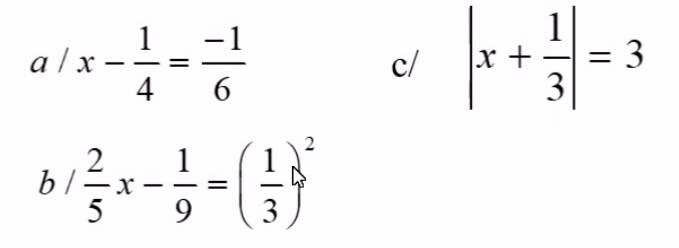a) \(x-\dfrac{1}{4}=-\dfrac{1}{6}\Leftrightarrow x=-\dfrac{1}{6}+\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{12}\)
b) \(\dfrac{2}{5}x-\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\Leftrightarrow\dfrac{2}{5}x=\dfrac{1}{9}+\dfrac{1}{9}\Leftrightarrow\dfrac{2}{5}x=\dfrac{2}{9}\Leftrightarrow x=\dfrac{5}{9}\)
c) \(\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3-\dfrac{1}{3}\\x=-3-\dfrac{1}{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
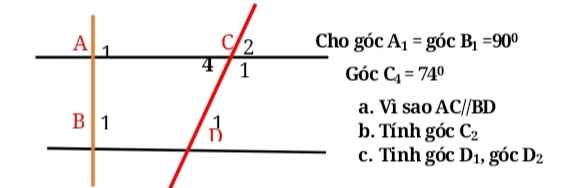
\(\left(a\right)\)
\(x-\dfrac{1}{4}=\dfrac{-1}{6}\)
\(x=\dfrac{1}{12}\)
/\(x+\dfrac{1}{3}\)/=3
=> \(x+\dfrac{1}{3}=3\) hoặc \(-x-\dfrac{1}{3}=3\)
=> x=\(\dfrac{8}{3}\) hoặc x= \(\dfrac{-10}{3}\)
a: Ta có: \(x-\dfrac{1}{4}=-\dfrac{1}{6}\)
\(\Leftrightarrow x=\dfrac{1}{4}-\dfrac{1}{6}\)
hay \(x=\dfrac{1}{12}\)
b: Ta có: \(\dfrac{2}{5}x-\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\)
\(\Leftrightarrow x\cdot\dfrac{2}{5}=\dfrac{1}{9}+\dfrac{1}{9}=\dfrac{2}{9}\)
hay \(x=\dfrac{5}{9}\)
c: Ta có: \(\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)