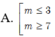Các câu hỏi tương tự
Giá trị m để đường thẳng
y
2
x
+
m
cắt đường cong
y
x
+
1
x
-
1
tại hai điểm A, B phân biệt sao cho đoạn AB ngắn nhất là A.
m
≠
-
1
B.
m
-
1
C.
m
-
1
D.
∀
m
∈...
Đọc tiếp
Giá trị m để đường thẳng y = 2 x + m cắt đường cong y = x + 1 x - 1 tại hai điểm A, B phân biệt sao cho đoạn AB ngắn nhất là
A. m ≠ - 1
B. m = - 1
C. m < - 1
D. ∀ m ∈ ℝ
Cho hàm số
y
2
x
+
3
x
+
2
có đồ thị (C) và đường thẳng d:
y
x
+
m
Các giá trị của tham số m để đường thẳng (C) cắt đồ thị tại hai điểm phân biệt là: A.
m
2
B.
m
6
C.
m
2
D.
m...
Đọc tiếp
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d: y = x + m Các giá trị của tham số m để đường thẳng (C) cắt đồ thị tại hai điểm phân biệt là:
A. m > 2
B. m > 6
C. m = 2
D. m < 2 hoặc m > 6
Tập hợp tất cả các giá trị thực của tham số m để đường thẳng
y
−
2
x
+
m
cắt đồ thị của hàm số
y
x
+
1
x
−
2
tại hai điểm phân biệt là: A.
5
−
2
3...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = − 2 x + m cắt đồ thị của hàm số y = x + 1 x − 2 tại hai điểm phân biệt là:
A. 5 − 2 3 ; 5 + 2 3
B. − ∞ ; 5 − 2 6 ∪ 5 + 2 6 ; + ∞
C. − ∞ ; 5 − 2 3 ∪ 5 + 2 3 ; + ∞
D. − ∞ ; 5 − 2 6 ∪ 5 + 2 6 ; + ∞
Cho hàm số
y
x
+
1
x
−
2
Số các giá trị tham số m để đường thẳng
y
m
+
x
luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn
x
2
+
y
2
−
3...
Đọc tiếp
Cho hàm số y = x + 1 x − 2 Số các giá trị tham số m để đường thẳng y = m + x luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn x 2 + y 2 − 3 y = 4 là
A. 1
B. 0
C. 3
D. 2
Với giá trị nào của m thì đường thẳng
y
-
x
+
m
cắt đồ thị hàm số
C
:
y
x
-
2
1
-
x
tại hai điểm phân biệt là A. |m| 1 B. |m| 2 C.
m
≥
2
D. |m| 2
Đọc tiếp
Với giá trị nào của m thì đường thẳng y = - x + m cắt đồ thị hàm số C : y = x - 2 1 - x tại hai điểm phân biệt là
A. |m| < 1
B. |m| > 2
C. m ≥ 2
D. |m| < 2
Với giá trị nào của m thì đường thẳng
y
−
x
+
m
cắt đồ thị hàm số
C
:
y
x
−
2
1
−
x
tại hai điểm phân biệt là A.
m
2
B.
m
2
C.
m...
Đọc tiếp
Với giá trị nào của m thì đường thẳng y = − x + m cắt đồ thị hàm số C : y = x − 2 1 − x tại hai điểm phân biệt là
A. m > 2
B. m < 2
C. m ≥ 2
D. m < 1
Biết đồ thị (C) của hàm số
y
2
x
+
1
x
+
2
luôn cắt đường thẳng (d): y -x + m tại hai điểm phân biệt A, B.Tìm giá trị của tham số m để độ dài đoạn AB là ngắn nhất. B. m 1 C. m 0 D. m 4
Đọc tiếp
Biết đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng (d): y = -x + m tại hai điểm phân biệt A, B.Tìm giá trị của tham số m để độ dài đoạn AB là ngắn nhất.
![]()
B. m = 1
C. m = 0
D. m = 4
Tìm tất cả giá trị của tham số thực m để đường thẳng
d
:
y
x
+
m
cắt đồ thị hàm số
y
−
x
+
1
2
x
−
1
tại hai điểm phân biệt A, B. A.
m
0
B.
m
∈
ℝ
C. ...
Đọc tiếp
Tìm tất cả giá trị của tham số thực m để đường thẳng d : y = x + m cắt đồ thị hàm số y = − x + 1 2 x − 1 tại hai điểm phân biệt A, B.
A. m < 0
B. m ∈ ℝ
C. m > 1
D. m = 5
Tổng các giá trị của m để đường thẳng d:
y
-
x
+
m
cắt (C):
y
-
2
x
+
1
x
+
1...
Đọc tiếp
Tổng các giá trị của m để đường thẳng d: y = - x + m cắt (C): y = - 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho AB = 2 2 bằng
A. - 2
B. - 6
C. 0
D. - 1