Gấppppppppppp ạ 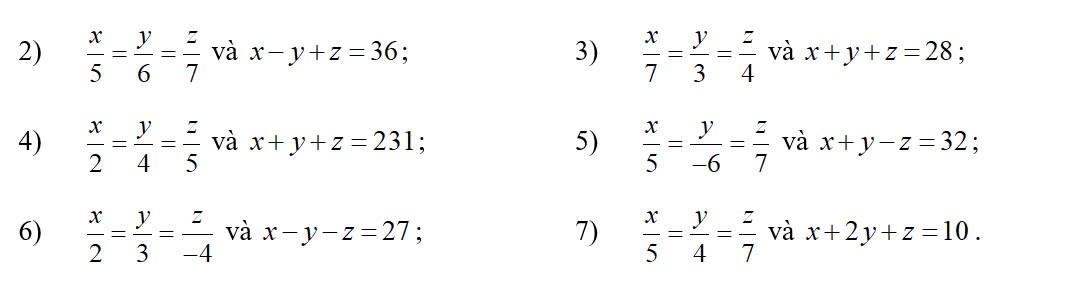
2) \(\frac{x}{5} = \frac{y}{6} = \frac{z}{7}\) và \(x - y + z = 36\);
3) \(\frac{x}{7} = \frac{y}{3} = \frac{z}{4}\) và \(x + y + z = 28\);
4) \(\frac{x}{2} = \frac{y}{4} = \frac{z}{5}\) và \(x + y + z = 231\);
5) \(\frac{x}{5} = \frac{y}{-6} = \frac{z}{7}\) và \(x + y - z = 32\);
6) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{-4}\) và \(x - y - z = 27\);
7) \(\frac{x}{5} = \frac{y}{4} = \frac{z}{7}\) và \(x + 2y + z = 10\).
\(2,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y+z}{5-6+7}=\dfrac{36}{6}=6\)
Do đó:
\(\dfrac{x}{5}=6\) nên \(x=6.5=30\)
\(\dfrac{y}{6}=6\) nên \(y=6.6=36\)
\(\dfrac{z}{7}=6\) nên \(z=6.7=42\)
Vậy \(x=30;y=36;z=42\)
\(3,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{7+3+4}=\dfrac{28}{14}=2\)
Do đó:
\(\dfrac{x}{7}=2\) nên \(x=2.7=14\)
\(\dfrac{y}{3}=2\) nên \(y=2.3=6\)
\(\dfrac{z}{4}=2\) nên \(z=2.4=8\)
Vậy \(x=14;y=6;z=8\)
\(4,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{2+4+5}=\dfrac{231}{11}=21\)
Do đó:
\(\dfrac{x}{2}=21\) nên \(x=21.2=42\)
\(\dfrac{y}{4}=21\) nên \(y=21.4=84\)
\(\dfrac{z}{5}=21\) nên \(z=21.5=105\)
Vậy \(x=42;y-84;z=105\)
\(5,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x+y-z}{5+\left(-6\right)-7}=\dfrac{32}{-8}=-4\)
Do đó:
\(\dfrac{x}{5}=-4\) nên \(x=-4.5=-20\)
\(\dfrac{y}{-6}=-4\) nên \(y=-4.\left(-6\right)=24\)
\(\dfrac{z}{7}=-4\) nên \(x=-4.7=-28\)
Vậy \(x=-20;y=24;z=-28\)
2: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y+z}{5-6+7}=\dfrac{36}{6}=6\)
=>\(\left\{{}\begin{matrix}x=6\cdot5=30\\y=6\cdot6=36\\z=6\cdot7=42\end{matrix}\right.\)
3: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{7+3+4}=\dfrac{28}{14}=2\)
=>\(\left\{{}\begin{matrix}x=2\cdot7=14\\y=2\cdot3=6\\z=2\cdot4=8\end{matrix}\right.\)
4: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{2+4+5}=\dfrac{231}{11}=21\)
=>\(\left\{{}\begin{matrix}x=21\cdot2=42\\y=21\cdot4=84\\z=21\cdot5=105\end{matrix}\right.\)
5: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x+y-z}{5+\left(-6\right)-7}=\dfrac{32}{-8}=-4\)
=>\(\left\{{}\begin{matrix}x=-4\cdot5=-20\\y=\left(-4\right)\cdot\left(-6\right)=24\\z=-4\cdot7=-28\end{matrix}\right.\)
6: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{-4}=\dfrac{x-y-z}{2-3-\left(-4\right)}=\dfrac{27}{-1+4}=\dfrac{27}{3}=9\)
=>\(\left\{{}\begin{matrix}x=9\cdot2=18\\y=9\cdot3=27\\z=9\cdot\left(-4\right)=-36\end{matrix}\right.\)
7: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{7}=\dfrac{x+2y+z}{5+2\cdot4+7}=\dfrac{10}{20}=\dfrac{1}{2}\)
=>\(\left\{{}\begin{matrix}x=5\cdot\dfrac{1}{2}=\dfrac{5}{2}\\y=4\cdot\dfrac{1}{2}=2\\z=7\cdot\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)
\(6,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{-4}=\dfrac{x-y-z}{2-3-\left(-4\right)}=\dfrac{27}{3}=9\)
Do đó:
\(\dfrac{x}{2}=9\) nên \(x=9.2=18\)
\(\dfrac{y}{3}=9\) nên \(y=9.3=21\)
\(\dfrac{z}{-4}=9\) nên \(z=9.\left(-4\right)=-36\)
Vậy \(x=18;y=21;z=-36\)
\(7,\) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{7}=\dfrac{x}{5}=\dfrac{2y}{8}=\dfrac{z}{7}=\dfrac{x+2y+z}{5+8+7}=\dfrac{10}{20}=0,5\)
Do đó:
\(\dfrac{x}{5}=0,5\) nên \(x=0,5.5=2,5\)
\(\dfrac{y}{4}=0,5\) nên \(y=0,5.4=2\)
\(\dfrac{z}{7}=0,5\) nên \(z=0,5.7=3,5\)
Vậy \(x=2,5;y=2;z=3,5\)








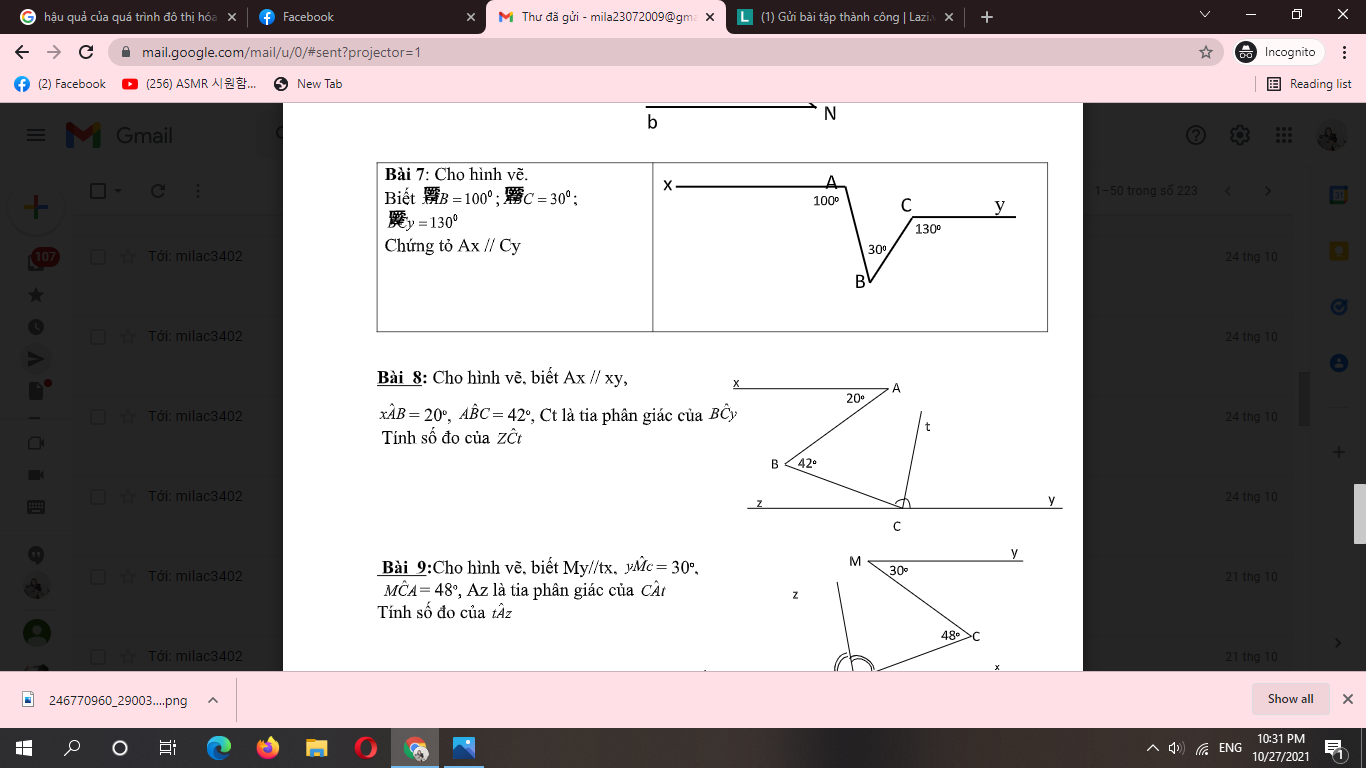 hộ bài 7 ạ nhanh ạ làm luôn đi ạ đừng ns j linh tinh ạ
hộ bài 7 ạ nhanh ạ làm luôn đi ạ đừng ns j linh tinh ạ



 vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
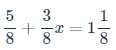
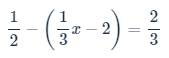
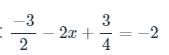
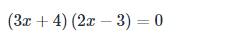
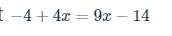
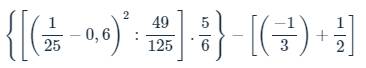 ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!
ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!




 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ