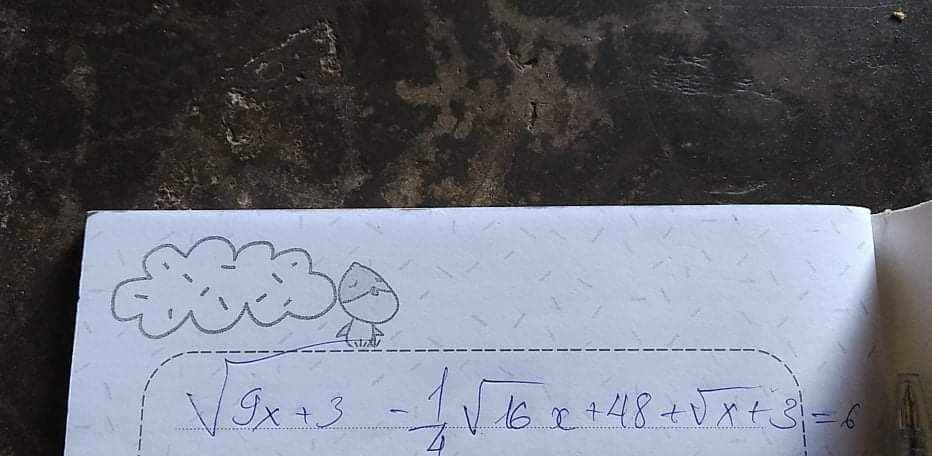Bổ đề đơn giản: chỉ tồn tại đúng 2 số tự nhiên liên tiếp là 2 lập phương, đó là 0 và 1
Chứng minh rất đơn giản, \(x=m^3\) thì \(x+1=n^3\Rightarrow m^3=n^3-1\) với m;n; x là các số tự nhiên
\(\Leftrightarrow\left(n-m\right)\left(n^2-mn+m^2\right)=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}n-m=1\\n^2-mn+m^2=1\end{matrix}\right.\) \(\Rightarrow n=1;m=0\)
Theo t/c hàm phần nguyên: \(\left\{{}\begin{matrix}a^3+3a^2b-1< \left[a^3+3a^2b\right]\le a^3+3a^2b\\b^3+3ab^2-1< \left[b^3+3ab^2\right]\le b^3+3ab^2\end{matrix}\right.\)
Cộng vế:
\(\Rightarrow\left(a+b\right)^3-2< \left[a^3+3a^2b\right]+\left[b^3+3ab^2\right]\le\left(a+b\right)^3\)
Do \(\left[a^3+3a^2b\right]+\left[b^3+3ab^2\right]\) là 1 lập phương nên hiển nhiên nó là số nguyên
\(\Rightarrow\left[{}\begin{matrix}\left[a^3+3a^2b\right]+\left[a^3+3ab^2\right]=\left(a+b\right)^3-1\left(1\right)\\\left[a^3+3a^2b\right]+\left[a^3+3ab^2\right]=\left(a+b\right)^3\end{matrix}\right.\)
Nếu 1 xảy ra đồng nghĩa \(\left(a+b\right)^3-1\) là 1 lập phương, mà \(\left(a+b\right)^3\) hiển nhiên cũng là 1 lập phương
Theo bổ đề trên, suy ra \(\left\{{}\begin{matrix}\left(a+b\right)^3-1=0\\\left(a+b\right)^3=1\end{matrix}\right.\)
\(\Rightarrow a+b=1\)
\(\Rightarrow\left\{{}\begin{matrix}0< a< 1\\0< b< 1\end{matrix}\right.\) \(\Rightarrow0< ab< 1\Rightarrow ab\) ko phải số nguyên, trái giả thiết
Vậy \(\left[a^3+3a^2b\right]+\left[a^3+3ab^2\right]=\left(a+b\right)^3\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[a^3+3a^2b\right]=a^3+3a^2b\\\left[a^3+3ab^2\right]=b^3+3ab^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^3+3a^2b\in Z\\b^3+3ab^2\in Z\end{matrix}\right.\)
Trừ vế: \(a^3-b^3+3a^2b-3ab^2\in Z\)
\(\Leftrightarrow\left(a-b\right)\left[\left(a+b\right)^2+2ab\right]\in Z\)
\(\Rightarrow a-b\in Q\) \(\Rightarrow\left\{{}\begin{matrix}2a\in Q\\2b\in Q\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a\in Q\\b\in Q\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{x}{y}\\b=\dfrac{m}{n}\end{matrix}\right.\) với x;y;m;n là các số nguyên dương và \(\left\{{}\begin{matrix}\left(x,y\right)=1\\\left(m,n\right)=1\end{matrix}\right.\)
Ta có: \(a+b=\dfrac{x}{y}+\dfrac{m}{n}\in Z\Rightarrow n\left(a+b\right)=m+n.\dfrac{x}{y}\in Z\)
Do x;y nguyên tố cùng nhau \(\Rightarrow n\) chia hết cho y (1)
Tương tự, từ \(a+b=\dfrac{x}{y}+\dfrac{m}{n}\in Z\Rightarrow y\left(a+b\right)=x+y.\dfrac{m}{n}\in Z\)
Do m;n nguyên tố cùng nhau \(\Rightarrow y\) chia hết cho n (2)
(1);(2) \(\Rightarrow n=y\Rightarrow\left\{{}\begin{matrix}a=\dfrac{x}{y}\\b=\dfrac{m}{y}\end{matrix}\right.\) với \(\left(x,y\right)=\left(m,y\right)=1\)
Nếu \(y\ne1\)
Gọi p là 1 ước nguyên tố của y, do \(\left(x,y\right)=\left(m,y\right)=1\Rightarrow x;m\) đều ko chia hết cho p
\(\Rightarrow x.m\) ko chia hết cho p
\(\Rightarrow ab=\dfrac{xm}{y^2}=\dfrac{x.m}{k.p^2}\) ko phải số nguyên do \(x.m\) ko chia hết cho p, trái giả thiết
Vậy \(y=1\Rightarrow\left\{{}\begin{matrix}a=x\in Z\\b=m\in Z\end{matrix}\right.\)
Hay a;b đều là số nguyên
đợt sau lấy đề thì tôi tính tiền bản quyền nhé ^^
2.
Với \(p=\left\{3;5;7;13\right\}\) thỏa mãn
Với \(p>13\), giả sử p là số nguyên tố thỏa mãn yêu cầu đề bài.
Xét số nguyên dương \(p-4\)
Nếu \(p-4\) có ít nhất 1 ước nguyên tố \(q>4\), hay \(p-4\) chia hết cho q
Suy ra \(p\) chia \(q\) dư \(4=2^2\) không thỏa mãn
Do đó, \(p-4\) không có ước nguyên tố nào lớn hơn 4, mặt khác p lẻ nên \(p-4\) lẻ, do đó \(p-4\) ko chia hết cho 2
Suy ra \(p-4\) chỉ có đúng 1 ước nguyên tố là 3
Hay \(p-4=3^k\Rightarrow p=3^k+4\) với \(k>2\)
- Xét số \(p-8\), với lý luận tương tự, nếu \(p-8\) có bất kì ước nguyên tố q lớn hơn 8 nào, thì p chia q dư \(8=2^3\) (ktm)
Nên \(p-8\) chỉ có các ước nguyên tố nhỏ hơn 8.
p lẻ nên \(p-8\) ko chia hết cho 2. Đồng thời \(p-8=3^k+4-8=3^k-4\) ko chia hết cho 3 do 4 ko chia hết cho 3
Vậy \(p-8\) chỉ có thể có ước nguyên tố 5 hoặc 7 (hoặc cả 2, ko quan trọng) (1)
- Xét số \(p-9\), tương tự ta có \(p-9\) chỉ có các ước nguyên tố nhỏ hơn 9.
Đồng thời \(p-9=3^k-5\) ko chia hết cho 3 (do 5 ko chia hết cho 3) và ko chia hết cho 5 (do \(3^k\) ko chia hết cho 5)
Nên \(p-9\) chỉ có thể có các ước nguyên tố thuộc 2 hoặc 7
Nếu \(p-9\) chia hết cho 7, suy ra \(p-8\) ko chia hết cho 7 (do 2 số tự nhiên liên tiếp ko thể đồng thời chia hết cho 7)
Nếu \(p-9\) không chia hết cho 7, khi đó \(p-9\) chỉ có đúng 1 ước nguyên tố là 2.
Do đó \(p-9=2^n\) \(\Rightarrow p-8=2^n+1\). Ta có \(2^n+1\) chia 7 chỉ có các số dư 2,3,5 với mọi n tự nhiên, hay \(p-8=2^n+1\) ko chia hết cho 7 với mọi n
\(\Rightarrow p-8\) ko có ước nguyên tố là 7 (2)
(1);(2) \(\Rightarrow p-8\) chỉ có đúng 1 ước nguyên tố là 5
Hay \(p-8=5^n\) \(\Rightarrow p=5^n+8\Rightarrow3^k+4=5^n+8\)
\(\Rightarrow3^k-4=5^n\)
Nếu k lẻ thì \(3^k\) chia 5 dư 2 hoặc 3, suy ra \(3^k-4\) ko chia hết cho 5 (ktm)
Nên k chẵn, hay \(k=2a\)
\(\Rightarrow3^{2a}-4=5^n\) \(\Leftrightarrow\left(3^a-2\right)\left(3^a+2\right)=5^m\)
Do \(\left(3^a+2\right)-\left(3^a-2\right)=4\) ko chia hết cho 5 nên \(3^a+2\) và \(3^a-2\) ko thể đồng thời chia hết cho 5
\(\Rightarrow\left\{{}\begin{matrix}3^a-2=1\\3^a+2=5^m\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\m=1\end{matrix}\right.\) \(\Rightarrow k=2\) (ko thỏa mãn)
Vậy \(p=\left\{3;5;7;13\right\}\) là các giá trị thỏa mãn yêu cầu











 giúp em với ạ, mai em thi rồi
giúp em với ạ, mai em thi rồi


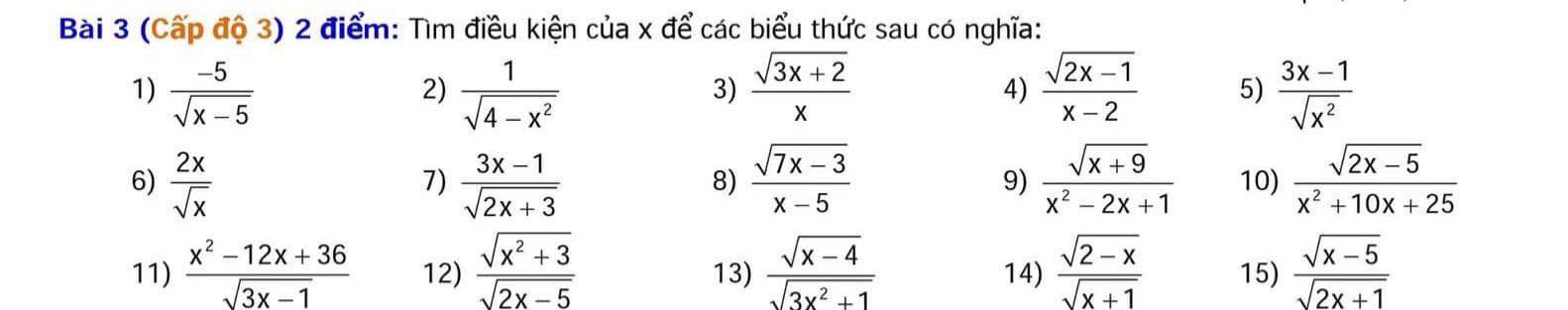

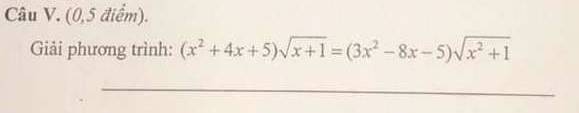





 Anh chị giúp em với ạ^^
Anh chị giúp em với ạ^^