a: Xét ΔMBA vuông tại B và ΔMCD vuông tại C có
MB=MC
\(\widehat{BMA}=\widehat{CMD}\)(hai góc đối đỉnh)
Do đó: ΔMBA=ΔMCD
=>BA=CD
Ta có: BA\(\perp\)AC
CD\(\perp\)AC
Do đó: BA//CD
Xét tứ giác BACD có
BA//CD
BA=CD
Do đó: BACD là hình bình hành
b: Ta có: BA//CD
=>BA//CE
Ta có: BA=CD
CD=CE
Do đó: BA=CE
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Hình bình hành ABCE có \(\widehat{CBA}=90^0\)
nên ABCE là hình chữ nhật
c: Xét ΔBCE có
CI,EM là các đường trung tuyến
CI cắt EM tại G
Do đó: G là trọng tâm của ΔBCE
=>\(IG=\dfrac{1}{3}CI\)
Xét ΔCBA có
BI,AM là các đường trung tuyến
BI cắt AM tại S
Do đó: S là trọng tâm của ΔCBA
=>\(SM=\dfrac{1}{3}AM\)
\(IG\cdot AD=\dfrac{1}{3}CI\cdot2\cdot AM=\dfrac{2}{3}\cdot CI\cdot AM\)
\(SM\cdot AC=\dfrac{1}{3}\cdot AM\cdot2\cdot CI=\dfrac{2}{3}\cdot AM\cdot CI\)
Do đó: \(IG\cdot AD=SM\cdot AC\)

 gấp ạaa 7h e cần r á..
gấp ạaa 7h e cần r á..





 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
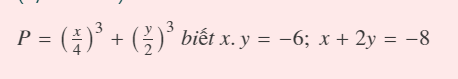
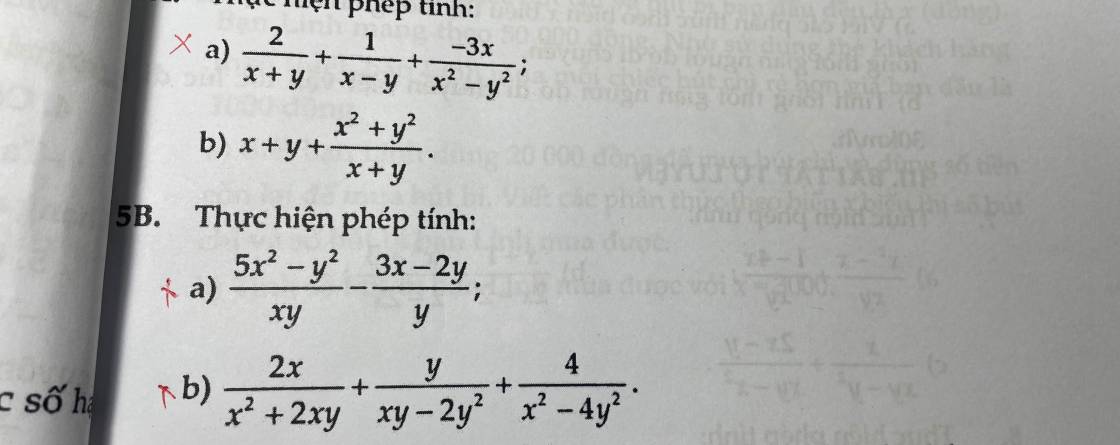

 nhanh mọi người ơi đang cần rất rất gấp luôn á
nhanh mọi người ơi đang cần rất rất gấp luôn á 




