a.
Do tam giác ABC vuông tại A (gt) \(\Rightarrow\widehat{A}=90^0\)
Do HE vuông góc AB (gt) \(\Rightarrow\widehat{AEH}=90^0\)
Do HF vuông góc AC (gt) \(\Rightarrow\widehat{AFH}=90^0\)
\(\Rightarrow AEHF\) là hình chữ nhật (tứ giác có 3 góc vuông)
b,
Do I là trung điểm BC \(\Rightarrow AI=\dfrac{1}{2}BC=BI\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow\Delta IAB\) cân tại I \(\Rightarrow\widehat{IAB}=\widehat{B}\) (1)
Theo cmt AEHF là hình chữ nhật \(\Rightarrow\widehat{FEA}=\widehat{HAE}\) (2)
Mà tam giác ABH vuông tại H nên \(\widehat{HAE}+\widehat{B}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{FEA}+\widehat{IAB}=90^0\)
\(\Rightarrow\widehat{AKE}=180^0-\left(\widehat{FEA}+\widehat{IAB}\right)=90^0\)
\(\Rightarrow AI\perp EF\) tại K






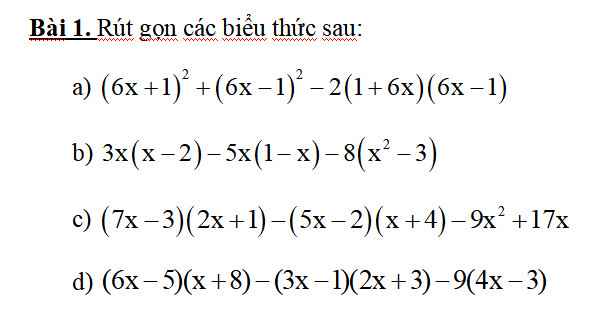
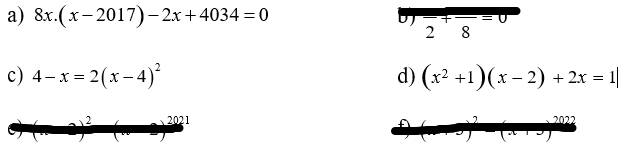
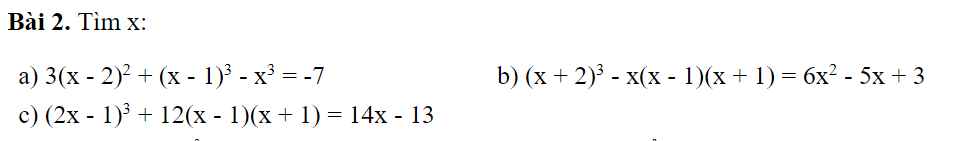 giúp với em sắp phải nộp deadline r ạ:((
giúp với em sắp phải nộp deadline r ạ:((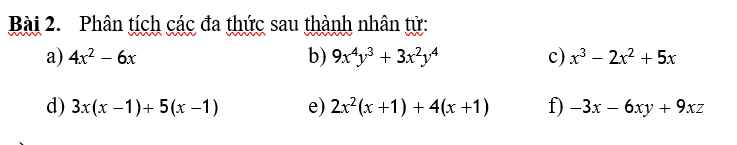



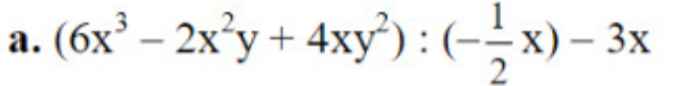 Cứu với ạ sắp tới hạn nộp r,xin cảm ơn rất rất nhiều
Cứu với ạ sắp tới hạn nộp r,xin cảm ơn rất rất nhiều


 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
