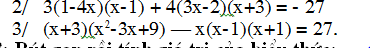a: Ta có: \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Leftrightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Leftrightarrow-9x=-18\)
hay x=2
b: ta có: \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3+x-6x^2+5x-3=0\)
\(\Leftrightarrow17x=-5\)
hay \(x=-\dfrac{5}{17}\)
c: Ta có: \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Leftrightarrow8x^3-12x^2+6x-1+12x^2-12-14x+13=0\)
\(\Leftrightarrow8x^3-8x=0\)
\(\Leftrightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
a) \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Rightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Rightarrow-9x=-18\)
\(\Rightarrow x=2\)
b) \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Rightarrow x^3+6x^2+12x+8-x^3+x=6x^2-5x+3\)
\(\Rightarrow18x=-5\)
\(\Rightarrow x=-\dfrac{5}{18}\)
c) \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Rightarrow8x^3-12x^2+6x-1+12x^2-12=14x-13\)
\(\Rightarrow8x^3-8x=0\)
\(\Rightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

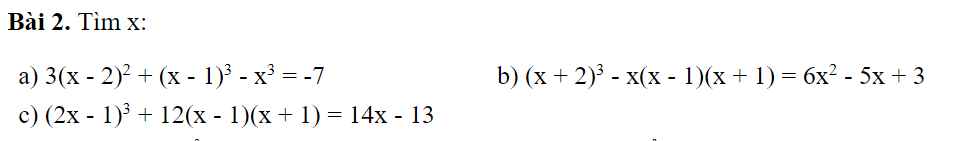 giúp với em sắp phải nộp deadline r ạ:((
giúp với em sắp phải nộp deadline r ạ:((