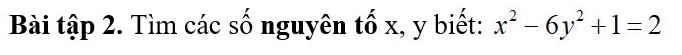Question

gaapspppppppppppppp:

Answer 1

\(x^2-6y^2+1=2\Leftrightarrow x^2-1=6y^2\)

\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=6y^2\)

- Với \(x=2\) ko thỏa mãn

- Với \(x\ne2\Rightarrow x\) lẻ (do x là số nguyên tố)

\(\Rightarrow x=2k+1\)

\(\Rightarrow2k\left(2k+2\right)=6y^2\)

\(\Rightarrow2k\left(k+1\right)=3y^2\)

\(\Rightarrow3y^2\) chẵn \(\Rightarrow y^2\) chẵn \(\Rightarrow y\) chẵn

\(\Rightarrow y=2\) (do y là số nguyên tố)

Thay vào pt đầu:

\(x^2=6.2^2+1=25\Rightarrow x=5\)

Vậy \(\left(x;y\right)=\left(5;2\right)\)