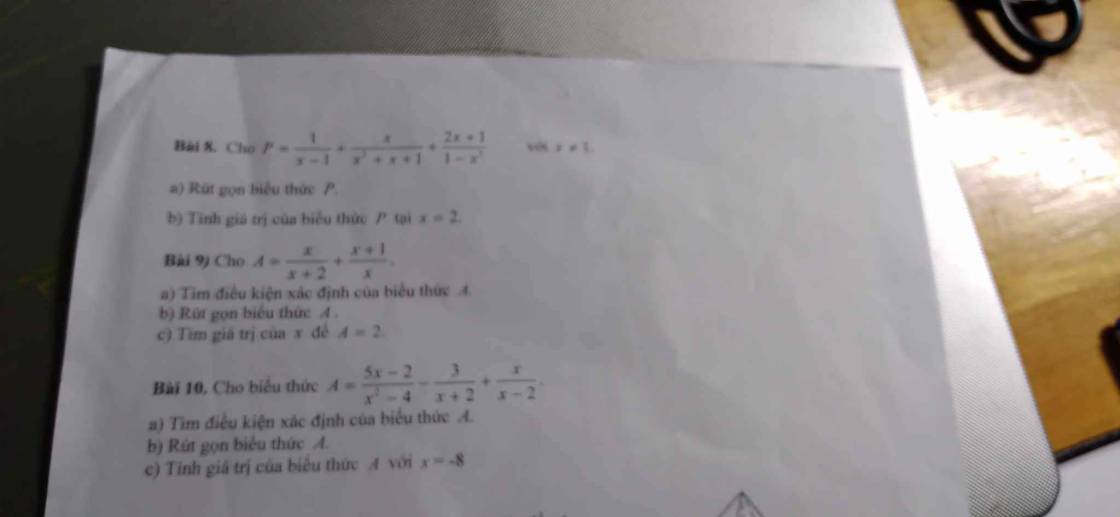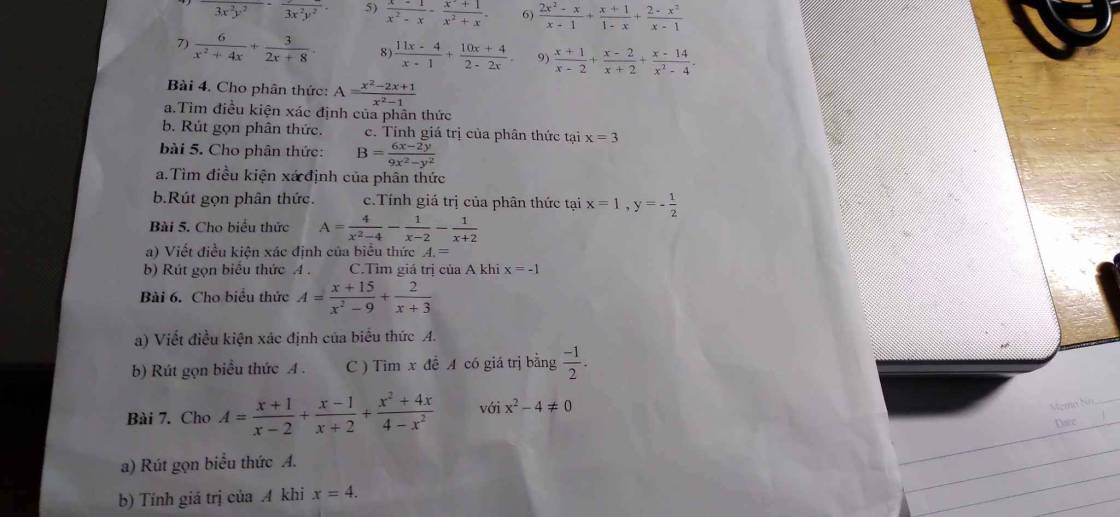7:
a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(A=\dfrac{x+1}{x-2}+\dfrac{x-1}{x+2}+\dfrac{x^2+4x}{4-x^2}\)
\(=\dfrac{x+1}{x-2}+\dfrac{x-1}{x+2}-\dfrac{x^2+4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+1\right)^2+\left(x-1\right)^2-x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x+1+x^2-2x+1-x^2-4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-4x+2}{\left(x-2\right)\left(x+2\right)}\)
b: Khi x=4 thì \(A=\dfrac{4^2-4\cdot4+2}{\left(4-2\right)\left(4+2\right)}=\dfrac{2}{2\cdot6}=\dfrac{1}{6}\)
Bài 6:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x^2-9< >0\\x+3< >0\end{matrix}\right.\Leftrightarrow x\notin\left\{3;-3\right\}\)
b: \(A=\dfrac{x+15}{x^2-9}+\dfrac{2}{x+3}\)
\(=\dfrac{x+15}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{x+3}\)
\(=\dfrac{x+15+2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x+9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x-3}\)
c: A=-1/2
=>\(\dfrac{3}{x-3}=\dfrac{-1}{2}\)
=>x-3=-6
=>x=-3(loại)