9.
a. Đúng
\(\left\{{}\begin{matrix}S\in\left(SAB\right)\cap\left(SCD\right)\\AB||CD\\AB\in\left(SAB\right);CD\in\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx||AB||CD\)
b. Sai
Tương tự câu a, ta có giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BD
Mà AD cắt AB nên giao tuyến này ko thể song song AB
c. Đúng
\(\left\{{}\begin{matrix}M\in\left(ABM\right)\\M\in SC\in\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow M\in\left(ABM\right)\cap\left(SCD\right)\)
\(\left\{{}\begin{matrix}AB||CD\\AB\in\left(ABM\right)\\CD\in\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow\left(ABM\right)\cap\left(SCD\right)=d\), với d là đường thẳng qua M và song song AB, CD
d. Đúng
Hoàn toàn tương tự câu c
10.
a. Đúng
\(S\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in CD\in\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b. Sai
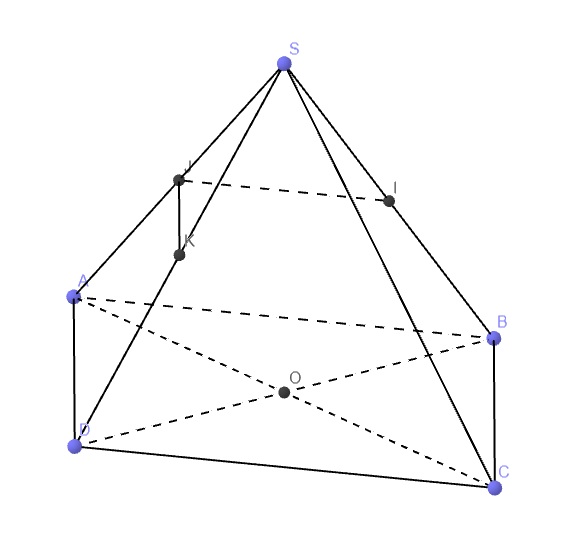
Trong mp (SAD), qua K kẻ đường thẳng d song song AD cắt SA tại J
\(KJ||AD\Rightarrow KJ||BC\)
Mà \(K\in\left(CKB\right)\Rightarrow KJ\in\left(CKB\right)\Rightarrow J\in\left(CKB\right)\)
\(\Rightarrow J=SA\cap\left(CKB\right)\)
Do \(KJ||AD\), mà AD cắt DC nên KJ ko song song DC
c. Đúng
\(O\in AC\Rightarrow C\in\left(OIA\right)\)
\(\Rightarrow C\in\left(SCD\right)\cap\left(OIA\right)\)
O là trung điểm BD, I là trung điểm SB nên OI là đường trung bình tam giác SBD
\(\Rightarrow OI||SD\)
\(\left\{{}\begin{matrix}C\in\left(SCD\right)\cap\left(OIA\right)\\OI||SD\\OI\in\left(OIA\right);SD\in\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow\left(OIA\right)\cap\left(SCD\right)=Cx||SD\)
d. Đúng
Theo câu b, K là trung điểm SD, mà \(KJ||AD\Rightarrow J\) là trung điểm SA
\(\Rightarrow IJ\) là đường trung bình tam giác SAB
\(\Rightarrow IJ||AB\Rightarrow IJ||CD\)
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
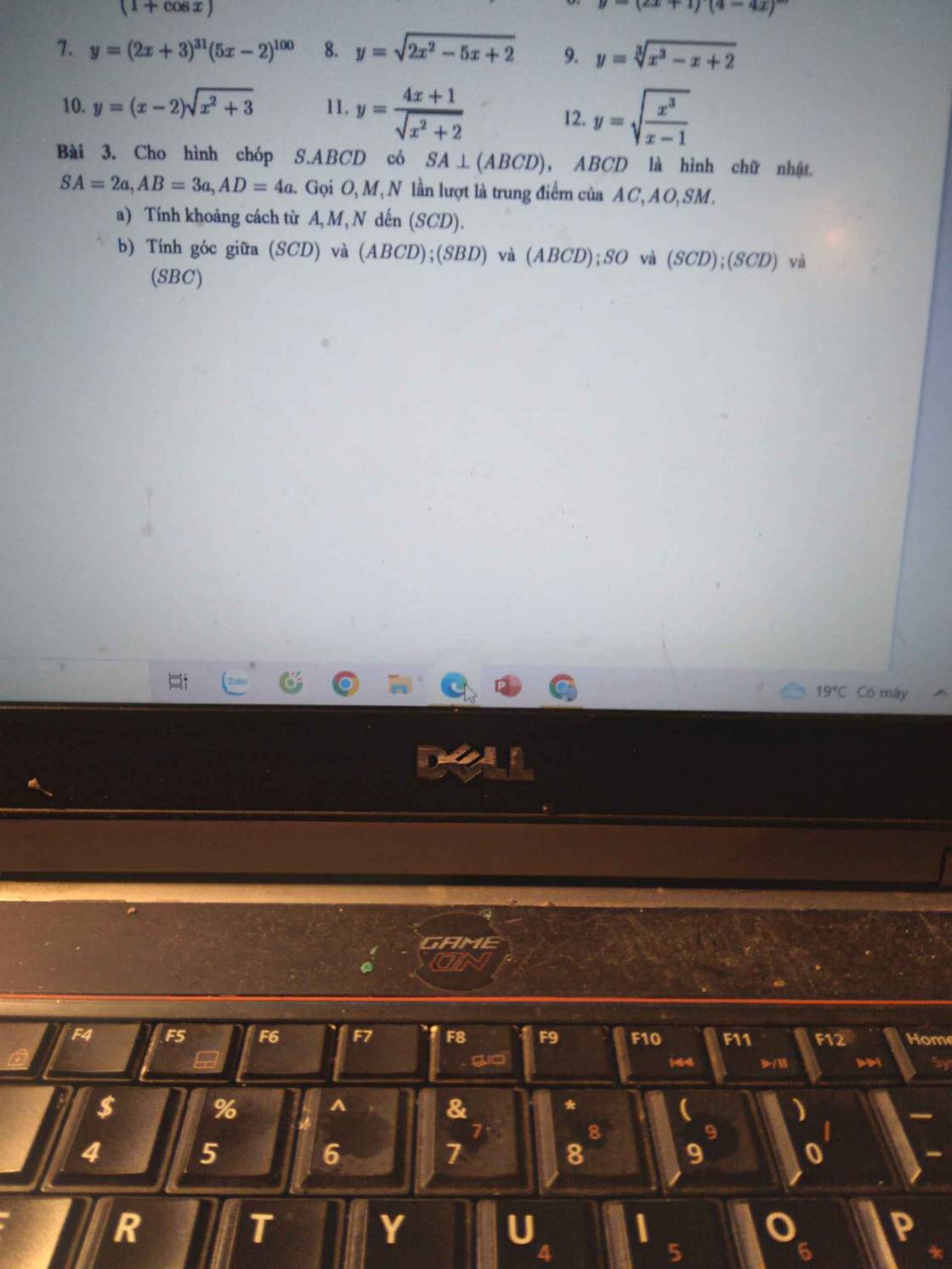Giúp em bài 3 với ạ. Em cảm ơn ạ
