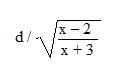đkxđ của bt:
\(\sqrt{\dfrac{x+1}{x-3}}\ne0\)
=> x khác 3
Lời giải:
ĐKXĐ: $x>3$ hoặc $x\leq -1$
Nếu $x>3$ thì pt trở thành:
$(x-3)(x+1)+4\sqrt{(x+1)(x-3)}+3=0$
Đặt $\sqrt{(x-3)(x+1)}=a(a\geq 0)$ thì pt trở thành:
$a^2+4a+3=0$
$\Leftrightarrow (a+1)(a+3)=0$
$\Leftrightarrow a=-1$ hoặc $a=-3$ (vô lý vì $a\geq 0$)
Nếu $x\leq -1$ thì pt trở thành:
$(x-3)(x+1)-4\sqrt{(3-x)^2}\sqrt{\frac{x+1}{x-3}}+3=0$
$\Leftrightarrow (x-3)(x+1)-4\sqrt{(x+1)(x-3)}+3=0$
Đặt $\sqrt{(x+1)(x-3)}=a(a\geq 0)$ thì pt trở thành:
$a^2-4a+3=0$
$\Leftrightarrow (a-1)(a-3)=0$
$\Leftrightarrow a=1$ hoặc $a=3$
Nếu $a=1$
$\Leftrightarrow a^2=1$ (do $a\geq 0$)
$\Leftrightarrow (x-3)(x+1)=1$
$\Leftrightarrow x^2-2x-4=0$
$\Leftrightarrow x=1- \sqrt{5}$ (do $x\leq -1$)
Nếu $a=3$
$\Leftrightarrow a^2=9$
$\Leftrightarrow (x-3)(x+1)=9$
$\Leftrightarrow x^2-2x-12=0$
$\Leftrightarrow x=1-\sqrt{13}$ (do $x\leq -1$)
ĐKXĐ: \(\left\{\begin{matrix} x-3\neq 0\\ \frac{x+1}{x-3}\geq 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x+1\geq 0\\ x-3>0\end{matrix}\right.\\ \left\{\begin{matrix} x+1\leq 0\\ x-3<0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x>3\\ x\leq -1\end{matrix}\right.\)






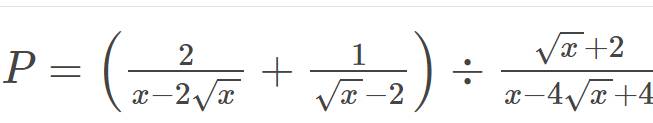 tìm điều kiện xác định và rút gọn ạaaa
tìm điều kiện xác định và rút gọn ạaaa


 Tìm điều kiện xác định
Tìm điều kiện xác định