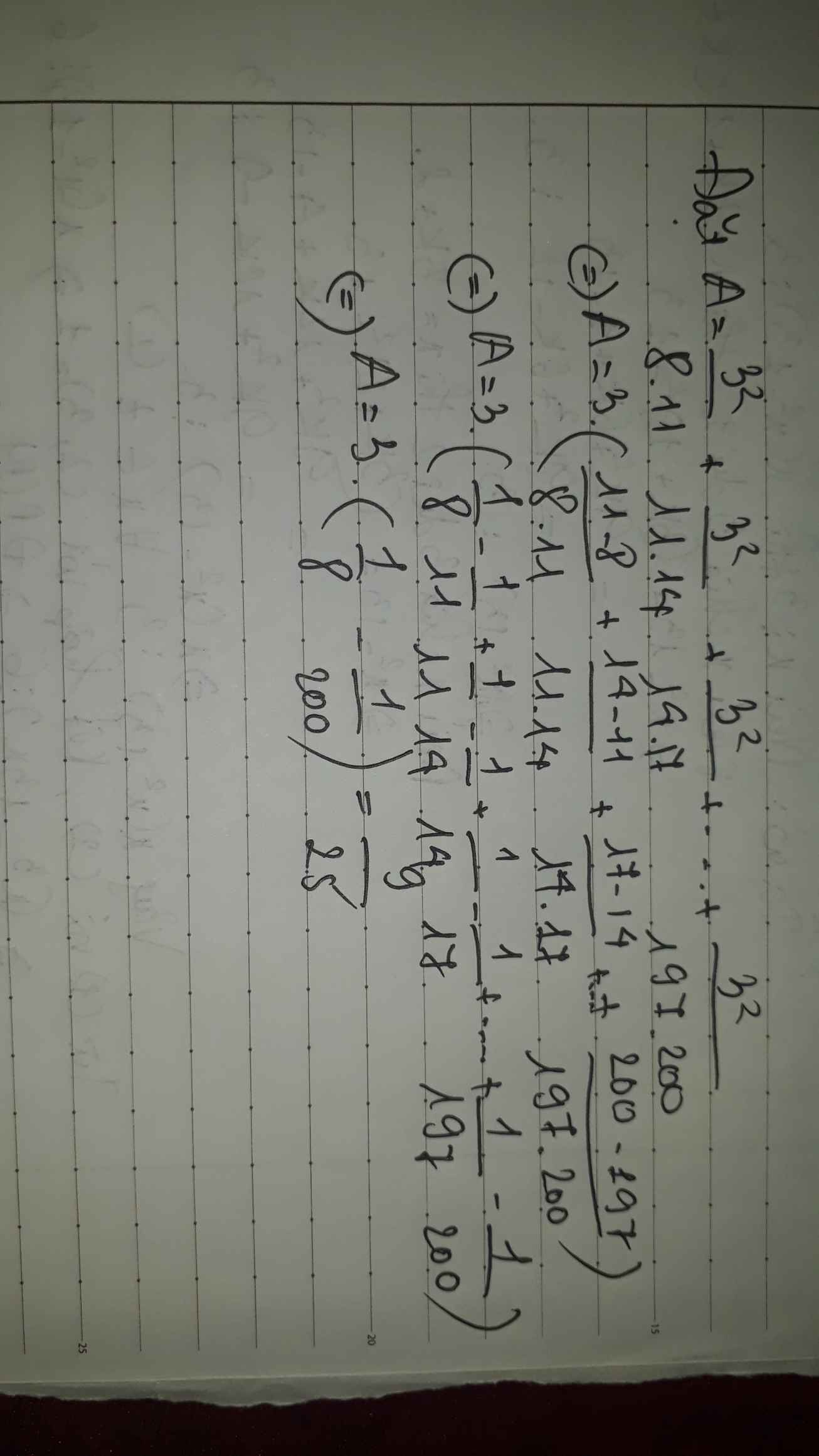Question

\(\dfrac{3^2}{8.11}+\dfrac{3^2}{11.14}+\dfrac{3^2}{14.17}+....+\dfrac{3^2}{197.200}\)

Answer 1

Answer 2

\(\dfrac{3^2}{8.11}+\dfrac{3^2}{11.14}+...+\dfrac{3^2}{197.200}\)

=\(3.\left(\dfrac{3}{8.11}+\dfrac{3}{11.14}+...+\dfrac{3}{197.200}\right)\)

=\(3.\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)

=\(3.\left(\dfrac{1}{8}-\dfrac{1}{200}\right)\)

=\(3.\dfrac{3}{25}=\dfrac{9}{25}\)

 

Answer 3

Ta có: \(\dfrac{3^2}{8\cdot11}+\dfrac{3^2}{11\cdot14}+\dfrac{3^2}{14\cdot17}+...+\dfrac{3^2}{197\cdot200}\)

\(=3\left(\dfrac{3}{8\cdot11}+\dfrac{3}{11\cdot14}+\dfrac{3}{14\cdot17}+...+\dfrac{3}{197\cdot200}\right)\)

\(=3\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)

\(=3\left(\dfrac{1}{8}-\dfrac{1}{200}\right)\)

\(=3\cdot\dfrac{24}{200}=\dfrac{72}{200}=\dfrac{9}{25}\)