Ta có lim 1 − 2 n 5 n + 5 n 2 = lim n 2 1 n 2 − 2 n n 2 5 n + 5 = lim 1 n 2 − 2 n 5 n + 5 = 0 5 = 0 .
Chọn đáp án D
Ta có lim 1 − 2 n 5 n + 5 n 2 = lim n 2 1 n 2 − 2 n n 2 5 n + 5 = lim 1 n 2 − 2 n 5 n + 5 = 0 5 = 0 .
Chọn đáp án D
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\sqrt{n^2-1}+3n\)
2) tính giới hạn I = \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+5}+n\right)\)
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
1. hàm số y = 3cosx luôn nhận giá trị trong tập nào
2. tập xác định của hàm số y = cosx
3. tính giới hạn \(L=\lim\limits\dfrac{n^2-3n^3}{2n^3+5n-2}\)
4. tính giới hạn \(L=\lim\limits\left(3n^2+5n-3\right)\)
5. kết quả của giới hạn \(\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\)
Cho M(2;–5); N(–3; 2), I(2;5). Đ I : M -> M’; Đ I : N -> N’. Tính tọa độ M ' N ' →
A. (5;7)
B. (7;5)
C.(5; –7)
D. (–7; 5)
Tính giới hạn a: lim n -> ∞ (3 ^ (2n) + 5) / (4 ^ (n + 2) - 9 ^ (n - 1))
Cho dãy số (\(u_n\)) xác định: \(\left\{{}\begin{matrix}u_1=5\\u_{n+1}=2u_n-3\end{matrix}\right.\).Tìm giới hạn lim(\(\dfrac{u_n}{2^n}\))
Cho tam giác ABC, điểm I thoả mãn: 5 M A → = 2 M B → . Nếu I A → = m I M → + n I B → thì cặp số (m; n) bằng:
A. 
B. 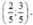
C. 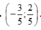
D. 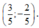
1.lim(\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{n\left(n+1\right)}\))
2.Tìm tất cả các giá trị của a sao cho lim\(\frac{4^n+a.5^n}{\left(2a-1\right).5^n+2^n}\)=1
3. Cho \(a\in R\)và lim(\(\sqrt{n^2+an+4}-n+1=5\)).Tìm a
4.Cho\(Lim_{(x->2)}f\left(x\right)=5\). Tìm giới hạn \(lim_{\left(x->2\right)}\sqrt{[f\left(x\right)-3]x}\)
Cho dãy số ( u n ) có u 1 = - 5 , u n + 1 = u n + 2 , n ∈ N * . Tổng S 5 = = u 1 + u 2 + . . . + u 5 bằng
A. 5
B. – 5
C. – 15
D. – 24