Chọn C.
Ta có : y’ = 4(x2 + 1)3(x2 + 1)’ = 8x(x2 + 1)3
⇒ y’(-1) = -64.
Chọn C.
Ta có : y’ = 4(x2 + 1)3(x2 + 1)’ = 8x(x2 + 1)3
⇒ y’(-1) = -64.
Đạo hàm của hàm số f ( x ) = ( x 2 + 1 ) 4 tại điểm x = - 1 là:
A. -32
B. 30
C. -64
D. 12
Đạo hàm của hàm số f ( x ) = x 2 + 1 4 tại điểm x = -1 là:
A. -32
B.30
C. - 64
D. 12
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Đạo hàm của hàm số f ( x ) = ( x 2 + 1 ) . ( 2 x - x 2 ) tại x = 0 là:
A. -4
B. 4
C. 2
D. 1
Đạo hàm của hàm số f ( x ) = ( x 2 + 1 ) . ( 2 x - x 2 ) tại x = 0 là:
A. -4
B. 4
C. 2
D. 1
Tìm a, b để hàm số f ( x ) = x 2 + x k h i x ≥ 1 a x + b k h i x < 1 có đạo hàm tại x = 1.
A. a = 23 b = - 1
B. a = 3 b = - 11
C. a = 33 b = - 31
D. a = 3 b = - 1
Tìm a, b để hàm số f ( x ) = x 2 + x k h i x ≥ 1 a x + b k h i x < 1 có đạo hàm tại x = 1.
A. a = 23 b = - 1
B. a = 3 b = - 11
C. a = 33 b = - 31
D. a = 3 b = - 1
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
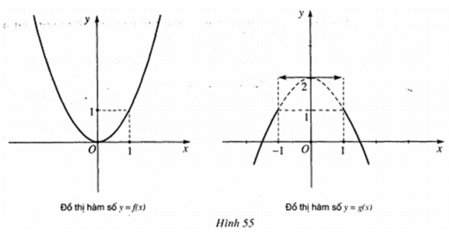
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .