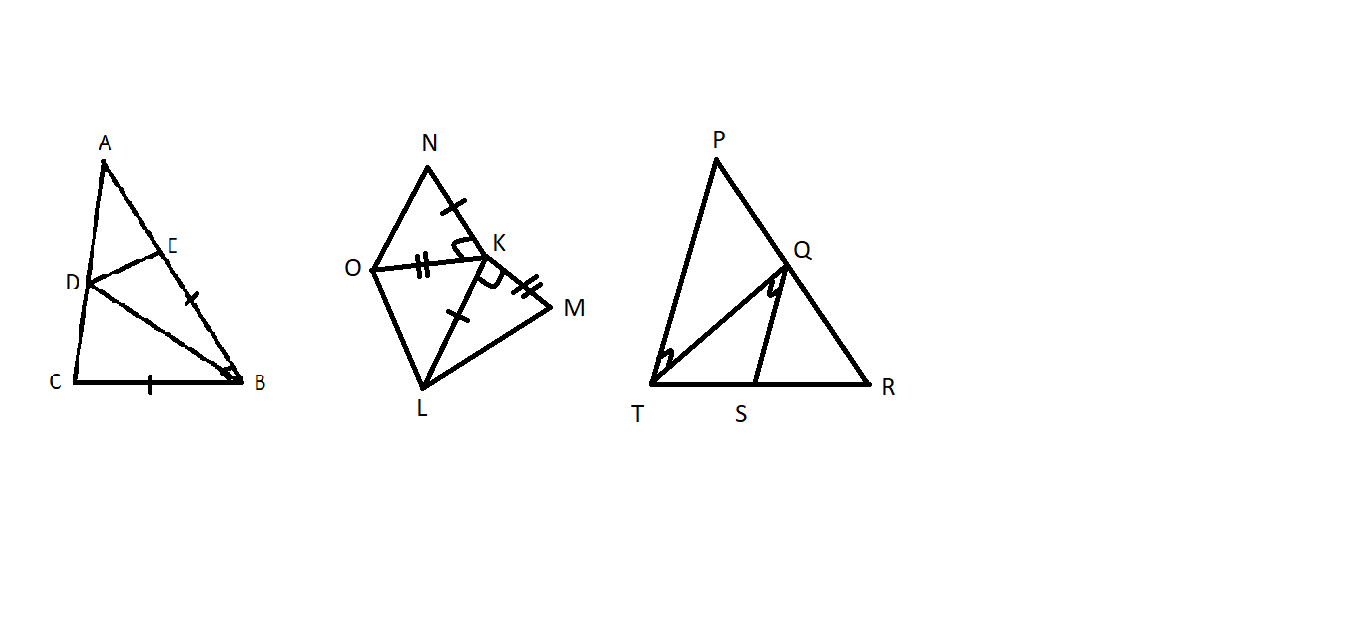
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Xét ΔAMD vuông tại A và ΔECD vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)
Do đó: ΔAMD=ΔECD
Suy ra: DM=DC
c: AD+EC=AD+AM>DM
Đúng 1
Bình luận (0)
a, Xét tg ABD và tg EBD có
g BAD = g BED ( =90 o)
BD chung
g ABD = g EBD ( GT )
\(\Rightarrow\) tg ABD = tg EBD ( g-c-g)
Đúng 0
Bình luận (0)
