a: Ta có: ΔABC vuông tại A
mà AO là đường trung tuyến
nên AO=OB=OC
=>A nằm trên (O)
Ta có: I là trung điểm của OA
=>OI+IA=OA
=>OI=OA-IA=R-r
=>(O) và (I) tiếp xúc với nhau tại O
b:
Xét (I) có
ΔAEO nội tiếp
AO là đường kính
Do đó: ΔAEO vuông tại E
=>OE\(\perp\)AC
Xét (O) có
ΔADO nội tiếp
AO là đường kính
Do đó: ΔADO vuông tại D
=>OD\(\perp\)AB
Ta có: OE\(\perp\)AC
AB\(\perp\)AC
Do đó: OE//AB
Ta có: OD\(\perp\)AB
AB\(\perp\)AC
Do đó: OD//AC
Xét ΔCAB có
O là trung điểm của CB
OE//AB
Do đó: E là trung điểm của AC
Xét ΔCAB có
O là trung điểm của CB
OD//AC
Do đó: D là trung điểm của AB
Xét (I) có
ΔAHO nội tiếp
AO là đường kính
Do đó: ΔAHO vuông tại H
=>AH\(\perp\)HO tại H
=>AH\(\perp\)BC tại H
=>ΔAHC vuông tại H
mà E là trung điểm của AC
nên Tâm của đường tròn ngoại tiếp ΔAHC là E, bán kính là EA
c: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{BC}{2}\)
d: K đối xứng A qua BC
=>BC là trung trực của AK
=>BC\(\perp\)AK tại trung điểm của AK
Ta có: BC\(\perp\)AK
BC\(\perp\)AH
AK,AH có điểm chung là A
Do đó: K,A,H thẳng hàng
=>BC cắt AK tại H
=>H là trung điểm của AK
Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
Để ΔCAK đều thì \(\widehat{ACK}=60^0\)
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot60^0=30^0\)

 cíu zới
cíu zới




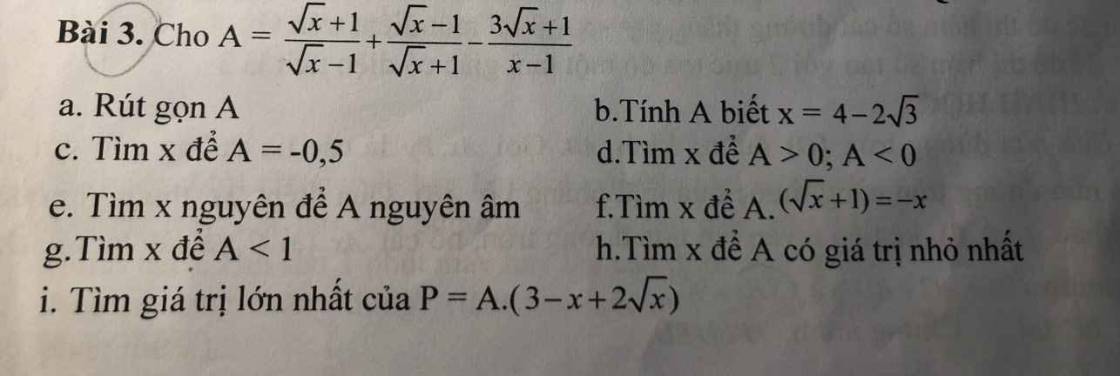 cíu cíu
cíu cíu cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 
