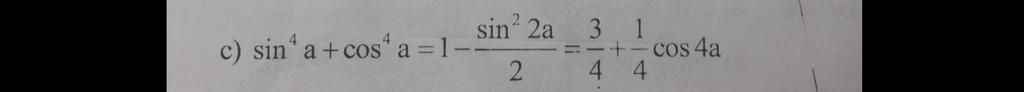\(sin^4a+cos^4a=\left(sin^2a+cos^2a\right)^2-2\cdot sin^2a\cdot cos^2a\)
\(=1-2\cdot\left(sina\cdot cosa\right)^2\)
\(=1-2\cdot\left(\dfrac{1}{2}\cdot sin2a\right)^2\)
\(=1-\dfrac{sin^22a}{2}\)
\(=\dfrac{3}{4}+\dfrac{1}{4}-\dfrac{1}{2}\cdot sin^22a=\dfrac{3}{4}+\dfrac{1}{4}\left(1-2\cdot sin^22a\right)\)
\(=\dfrac{3}{4}+\dfrac{1}{4}\cdot cos\left(2\cdot2a\right)=\dfrac{3}{4}+\dfrac{1}{4}\cdot cos4a\)
Ta có:
\(sin^4a+cos^4a=\left(sin^2a+cos^2a\right)^2-2sin^2a\cdot cos^2a\\ =1^2-2\left(\dfrac{2sina\cdot cosa}{2}\right)^2\\ =1-2\cdot\dfrac{sin^22a}{4}=1-\dfrac{sin^22a}{2}\\ =\dfrac{3}{4}+\left(\dfrac{1}{4}-\dfrac{sin^22a}{2}\right)\\ =\dfrac{3}{4}+\dfrac{1-2sin^22a}{4}\\ =\dfrac{3}{4}+\dfrac{cos4a}{4}=\dfrac{3}{4}+\dfrac{1}{4}cos4a\)