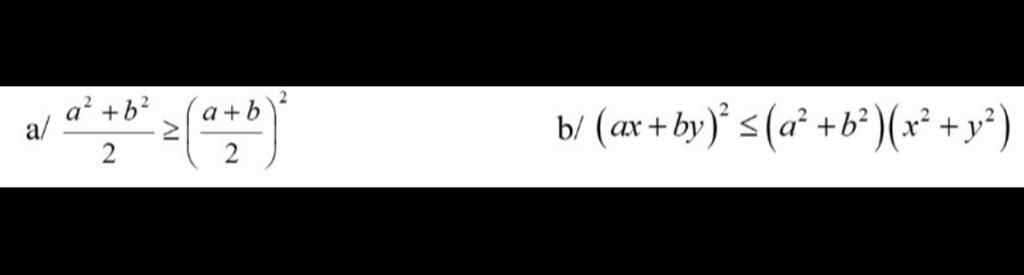\(a.\dfrac{a^2+b^2}{2}\ge\left(\dfrac{a+b}{2}\right)^2\\ \Leftrightarrow\dfrac{a^2+b^2}{2}\ge\dfrac{a^2+2ab+b^2}{4}\\ \Leftrightarrow2\left(a^2+b^2\right)\ge a^2+2ab+b^2\\ \Leftrightarrow a^2+b^2\ge2ab\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(\text{luôn đúng}\right)\)
Dấu "=" xảy ra khi: `a=b`
\(b.\left(ax+by\right)^2\le\left(a^2+b^2\right)\left(x^2+y^2\right)\\ < =>a^2x^2+2axby+b^2y^2\le a^2x^2+a^2y^2+x^2b^2+b^2y^2\\ < =>2axby\le x^2b^2+a^2y^2\\ < =>x^2b^2-2axby+a^2y^2\ge0\\ < =>\left(xb-ay\right)^2\ge0\left(\text{luôn đúng}\right)\)
Dấu "=" xảy ra khi: \(bx=ay\Leftrightarrow\dfrac{a}{x}=\dfrac{b}{y}\)