\(x^2+y^2=\left(x+y\right)^2-2xy=6\)
\(x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)=14\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2\left(xy\right)^2=34\)
\(\Rightarrow x^7+y^7=\left(x^3+y^3\right)\left(x^4+y^4\right)-\left(xy\right)^3\left(x+y\right)=478\)
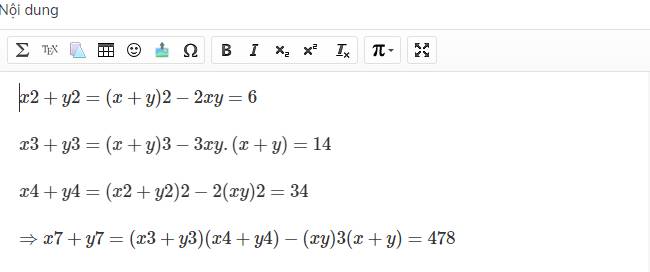 \(x2+y2=(x+y)2−2xy=6\)
\(x2+y2=(x+y)2−2xy=6\)
\(x3+y3=(x+y)3−3xy.(x+y)=14\)
\(x4+y4=(x2+y2)2−2(xy)2=34\)
\(⇒x7+y7=(x3+y3)(x4+y4)−(xy)3(x+y)=478\)
















