\(xy\le\dfrac{\left(x+y\right)^2}{4}=\dfrac{1}{4}\)
\(\Rightarrow P=xy+\dfrac{1}{xy}=xy+\dfrac{1}{16xy}+\dfrac{15}{16xy}\ge2\sqrt{xy.\dfrac{1}{16xy}}+\dfrac{15}{16.\dfrac{1}{4}}=\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
\(min_P=\dfrac{17}{4}\Leftrightarrow x=y=\dfrac{1}{2}\)










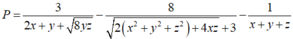 đạt giá trị nhỏ nhất. Tính
x
+
y
+
z
.
đạt giá trị nhỏ nhất. Tính
x
+
y
+
z
.